1. Ряд 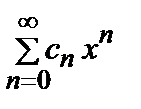 сходится абсолютно на любом отрезке [– a, а ], a > 0, где [– a, а ]
сходится абсолютно на любом отрезке [– a, а ], a > 0, где [– a, а ]  (– R, R), R > 0.
(– R, R), R > 0.
2. Сумма ряда S (x) = 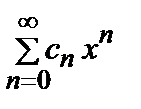 непрерывна в каждой точке х его интервала сходимости (– R, R), R > 0.
непрерывна в каждой точке х его интервала сходимости (– R, R), R > 0.
3. Степенной ряд 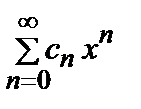 можно почленно интегрировать в его интервале сходимости (– R, R),
можно почленно интегрировать в его интервале сходимости (– R, R),
R > 0, причем радиус сходимости ряда, полученного почленным интегрированием, также равен R.
Для  х
х 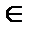 (– R, R) справедлива формула
(– R, R) справедлива формула
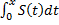 =
= 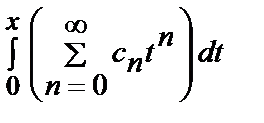 =
= 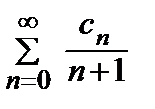 xn +1.
xn +1.
4. Степенной ряд 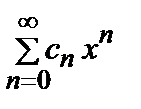 можно почленно дифференцировать в любой точке х его интервала сходимости (– R, R), R > 0, причем радиус сходимости ряда, полученного почленным дифференцированием, также равен R. При этом выполняется равенство
можно почленно дифференцировать в любой точке х его интервала сходимости (– R, R), R > 0, причем радиус сходимости ряда, полученного почленным дифференцированием, также равен R. При этом выполняется равенство
S´ (x) = 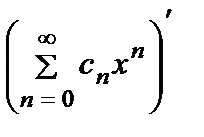 =
= 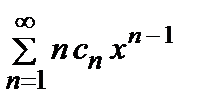 .
.
Следствие. Степенной ряд 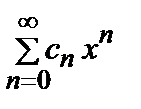 можно почленно дифференцировать сколько угодно раз в любой точке х его интервала сходимости (– R, R), R > 0, причем радиусы сходимости всех получаемых рядов будут равны R.
можно почленно дифференцировать сколько угодно раз в любой точке х его интервала сходимости (– R, R), R > 0, причем радиусы сходимости всех получаемых рядов будут равны R.
Контрольные вопросы
1. Может ли интервал сходимости ряда 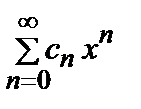 быть таким:
быть таким:
а) (–2, 0) Нет. б) (0, 2) Нет. в) (–3, 1) Нет. г) (–∞, ∞) Да. д) (–3, 3)? Да.
2. Известно, что ряд 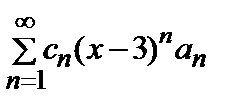 в точке х = 2 расходится. Что можно сказать о сходимости ряда
в точке х = 2 расходится. Что можно сказать о сходимости ряда
в точке а) х = 5Расходится б) х = 3,5 Ничего в) х = 4? Ничего
3. Известно, что ряд 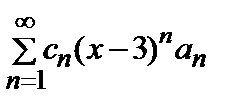 в точке х = 2 сходится абсолютно. Что можно сказать о
в точке х = 2 сходится абсолютно. Что можно сказать о
сходимости ряда в точке а) х = 5 Ничего б) х = 3,5Сходится абсолютно в) х = 4? Ничего
4. Существует ли степенной ряд, для которого верно следующее утверждение:
а) на обоих концах интервала сходимости ряд расходится; Да.
б) на одном конце интервала сходимости ряд сходится условно, на другом абсолютно;Нет.
в) на обоих концах интервала сходимости ряд сходится абсолютно;Да.
г) на одном конце интервала сходимости ряд сходится условно, на другом расходится;Да.
д) на одном конце интервала сходимости ряд сходится абсолютно, на другом расходится? Нет.
РЯД ТЕЙЛОРА
Рядом Тейлора функции f (x) относительно точки х 0 называется степенной ряд вида
f (x 0) + 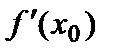 (x – x 0) +
(x – x 0) + 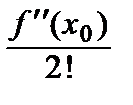 (x – x 0)2 + … +
(x – x 0)2 + … + 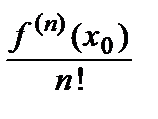 (x – x 0) n + … =
(x – x 0) n + … = 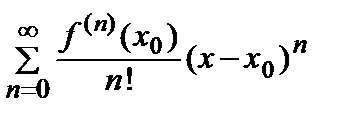 .
.
Коэффициенты этого ряда
с 0 = f (x 0), с 1 = 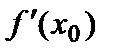 , с 2 =
, с 2 = 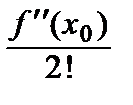 , сn =
, сn = 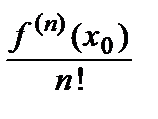 , …
, …
называются коэффициентами Тейлора функции f (x).
При х 0 = 0 ряд Тейлора называют рядом Маклорена:
f (0) + 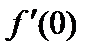 x +
x + 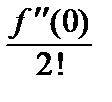 x 2 +
x 2 + 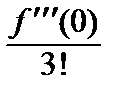 x 3 + … +
x 3 + … + 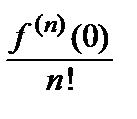 xn + … =
xn + … = 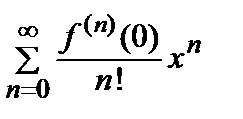 .
.
Теорема. Для того чтобы функцию f (x) можно было разложить в степенной ряд 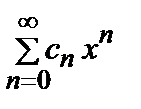 на интервале (– R, R), R > 0, необходимо и достаточно, чтобы на этом интервале функция f (x) имела производные всех порядков и
на интервале (– R, R), R > 0, необходимо и достаточно, чтобы на этом интервале функция f (x) имела производные всех порядков и
а) чтобы в ее формуле Тейлора остаточный член Rn (x) = f (x)– 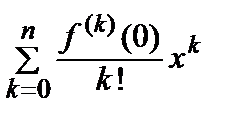 стремился к нулю
стремился к нулю
при n, стремящемся к бесконечности,  х
х 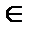 (– R, R) или
(– R, R) или
б) чтобы существовала constM > 0 такая, что | f ( n )(x) |≤ M для  n = 0, 1, 2, …и
n = 0, 1, 2, …и  х
х 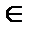 (– R, R).
(– R, R).
 2018-03-09
2018-03-09 555
555








