Ряды Тейлора элементарных функций

f ( x ) = e^x. Эта функция имеет производные всех порядков на интервале (– а, а), где а > 0 – любое число, причем | f ⁽ ⁿ ⁾(x) |= e^x < e^a, n = 0, 1, 2, …. Следовательно, показательная функция e^x разлагается в сходящийся к ней ряд Тейлора на любом интервале (– а, а) и, тем самым, на всей оси Ох.

Т.к. f ⁽ ⁿ ⁾(0) = e ⁰= 1 (n = 0, 1, 2, …), то получаем

e^x = 1 + х + + + … = .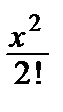

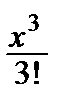Радиус сходимости этого ряда R =+∞.

Если в этом разложении заменить х на – х, то получим:

e ^– ^x = 1 – х + 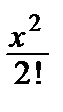– 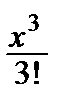+ … + (–1) ⁿ + … = .

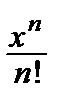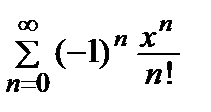f ( x ) = sin x. Эта функция имеет производные всех порядков на интервале (– а, а), где а > 0 – любое число, причем | f ⁽ ⁿ ⁾(x) |= | sin⁽ ⁿ ⁾(x) |= | sin (x + n 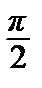) |≤1, n = 0, 1, 2, …. Следовательно, функция sin x разлагается в сходящийся к ней ряд Тейлора на интервале (– ∞, +∞).

Т.к. f ⁽ ⁿ ⁾(0) = 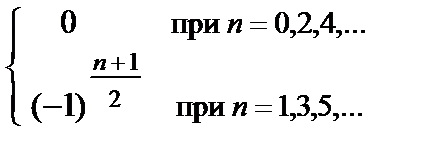, то этот ряд имеет следующий вид:

sin x = х – 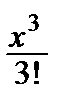+ – … + (–1) ⁿ + … = .

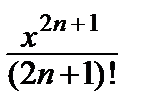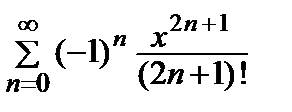Радиус сходимости этого ряда R =+∞.

f ( x ) = cos x. Аналогично получаем, что

cos x = 1– 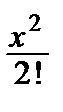+ 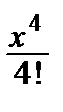– … + (–1) ⁿ + … = .

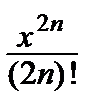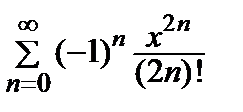Радиус сходимости этого ряда R =+∞.

f ( x ) = (1 + x ) ^α, α 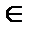R.Имеем:

а) 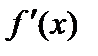= α (1 + x) ^α^– ¹, = α (α – 1)(1 + x) ^α^– ², …, f ⁽ ⁿ ⁾(x) = α (α – 1) … (α – (n – 1)) (1 + x) ^α^–ⁿ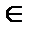, …, n N;

б) f (0) = 1, 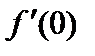= α, = α (α – 1), …, f ⁽ ⁿ ⁾(0) = α (α – 1) … (α – n + 1), ….

Составим ряд Тейлора для данной функции:

(1 + x) ^α ≈ 1 + αx + 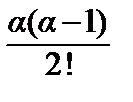x ² + 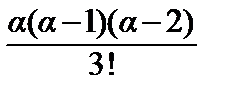x ³ +… + 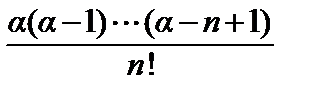xⁿ + …

R = 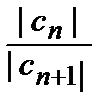= = 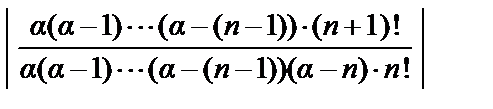= 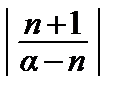1, т.е., составленный для функции

(1 + x) ^α ряд сходится в интервале (–1, 1).

Можно показать, что при х 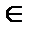(–1, 1) остаточный член стремится к нулю при n →∞. Следовательно,

(1 + x) ^α = 1 + αx + 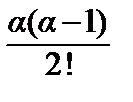x ² + 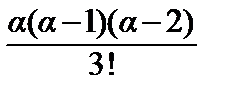x ³ + … + 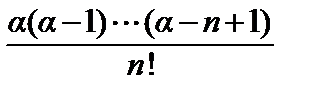xⁿ + …, где –1< x <1. (1)

Полученный ряд называется биномиальным, а его коэффициенты – биномиальными коэффициентами.

При α = –1 имеем:

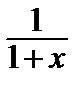= 1 – x + x ² – x ³ + …. (2)

Заменив х на – х, получим

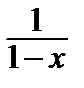= 1 + x + x ²+ x ³ + ….

f ( x ) = ln(1 + x ), x >–1.Проинтегрируем равенство (2) в пределах от 0 до х, где х 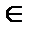(–1, 1). Имеем: 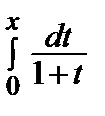= . Следовательно,

ln(1 + x) = х – 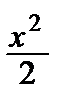+ 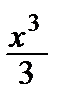– 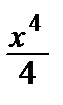+ … + (–1) ⁿ ^–1 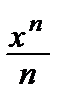+ …,–1< x <1.

ln(1 – x) = – х – 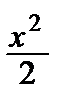– – 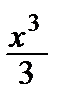– 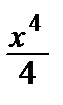… – – …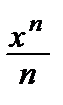,–1< x <1.

Отсюда ln2 = 1 – + – + ….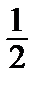

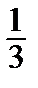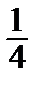f ( x ) = arctg x. Если в разложении (2) заменить х на х ², то получим

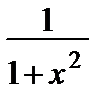= 1 – x ² + x ⁴ –…+ (–1) ⁿx ² ⁿ + …, х 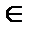(–1, 1).

Интегрируя обе части этого равенства в пределах от 0 до х, получим

arctg x = х – 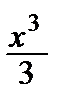+ 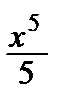– … + (–1) ⁿ 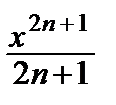+ … = 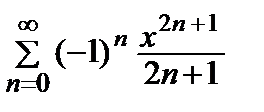, –1 ≤ x ≤ 1.

f ( x ) = arcsin x. Положив в формуле (1) α = – и заменив х на – х ², получим равенство:

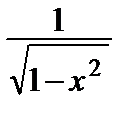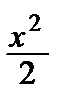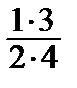= 1 + + x ⁴+ 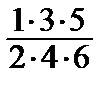x ⁶+ …, х 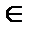(–1, 1).

Интегрируя обе части этого равенства в пределах от 0 до х, получим

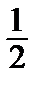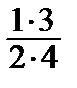
arcsin x = x + · + + 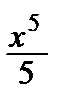…, –1 < x < 1.

Разложение функции в ряд Тейлора (Маклорена) возможно «в лоб», используя определение, как это делалось выше при разложении функций e^x, sin x, cos x, (1 + x) ^α. Но, как видно из других разложений, можно для этой цели воспользоваться уже известными разложениями. Для этого полученные разложения элементарных функций сведем в таблицу.