Знакочередующиеся ряды. Признак Лейбница

1 2 3 4 5 6 7

Числовой ряд

а ₁ – а ₂ + а ₃ – … + (–1) ⁿ ^–¹ а_n + …,

где все а_n ≥ 0, называется знакочередующимся.

Признак Лейбница

Теорема. Пусть в знакочередующемся ряде а ₁ – а ₂ + а ₃ – …

1) последовательность { а_n } убывает а ₁> а ₂> а ₃> … и

2) а_n = 0.

Тогда

1) этот ряд сходится,

2) его сумма S положительна и не превосходит первого члена 0< S ≤ а ₁.

⃰ Возьмем четную частичную сумму S ₂ _nэтого ряда и запишем ее в виде

S ₂ _n = (а ₁ – а ₂) + (а ₃ – а ₄) + (а ₅ – а ₆) + … + (а ₂ _n _–1 – а ₂ _n).

Из условия теоремы следует, что разности в скобках положительны и, значит, S ₂ _n > 0, причем

с возрастанием nчастичная сумма S ₂ _nвозрастает. Эту сумму можно записать и так:

S ₂ _n = а ₁ – (а ₂ – а ₃) – (а ₄ – а ₅) – … – (а ₂ _n _–2 – а ₂ _n _–1) – а ₂ _n.

Здесь каждая скобка тоже положительна и, следовательно, S ₂ _n < а ₁ (n = 1, 2, …).

Так как последовательность { S ₂ _n } монотонно возрастает и ограничена, то она имеет предел S ₂ _n = S, причем 0 < S ≤ а ₁.

Для нечетной частичной суммы S ₂ _n ₊₁ = а ₁ – (а ₂ – а ₃) – (а ₄ – а ₅) – … – (а ₂ _n – а ₂ _n ₊₁) имеем

S ₂ _n ₊₁ = S ₂ _n + а ₂ _n ₊₁ (n = 1, 2, …). По доказанному S ₂ _n = S, а по условию теоремы а ₂ _n ₊₁ = 0.

Поэтому существует предел S ₂ _n ₊₁ = S ₂ _n + а ₂ _n ₊₁ = S.

Т.о., доказано, что S_n = S, т.е. данный ряд сходится.

Из неравенства 0 < S ≤ а ₁ следует, во-первых, что S ≤ а ₁, и, во-вторых, положительность суммы ряда.

Замечания.

1. Теорема остается справедливой в части сходимости, если условие монотонности последовательности { а_n } будет выполняться для всех номеров n, начиная с некоторого номера N.

2. Теорема позволяет оценить n -й остаток R_n = ±(а_n ₊₁– а_n ₊₂+ …) рассматриваемого ряда, который также является знакочередующимся рядом.

3. Ряды, удовлетворяющие условиям теоремы Лейбница, называются рядами лейбницевскоготипа.

Пример 18. Исследовать на сходимость ряд .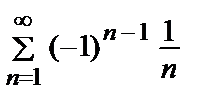

• НПС: 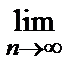a_n = 0. Может как сходиться, так и расходиться.

Ряд знакочередующийся. Проверяем его на выполнение условий Лейбница:

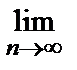
1) 1 > > > …. 2) = 0.

Ряд лейбницевского типа. Сходится.

Пример 19. Вычислить приближенно сумму ряда 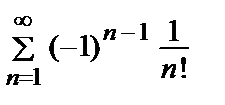, ограничившись четырьмя членами, и оценить

погрешность.

• НПС: 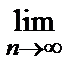a_n = 0. Может как сходиться, так и расходиться.

Ряд знакочередующийся. Проверяем его на выполнение условий Лейбница:

1) 1 > > > 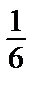…. 2)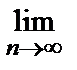 = 0.

Ряд лейбницевского типа. Сходится.

S ≈ S ₄ = 1 – + 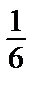– = 0,625.

Абсолютная погрешность | S – S ₄ | ≤ = 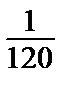≈ 0,0083.

ЗНАКОПЕРЕМЕННЫЕ РЯДЫ

Числовой ряд 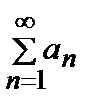, где а_n может быть любого знака, называется знакопеременным.

Утверждение 1. Если сходится ряд , то сходится и ряд .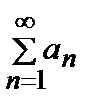

⃰ Из сходимости большего ряда следует сходимость меньшего ряда.

Ряд является рядом с положительными членами, поэтому при его исследовании на сходимость можно применять все признаки сходимости для знакоположительных рядов.

Определение: Знакопеременный ряд 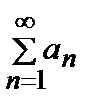называется абсолютно сходящимся, если сходится ряд . Знакопеременный ряд 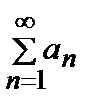называется условно сходящимся, если он сходится, а ряд расходится.

При исследовании знакопеременного ряда на сходимость в первую очередь проверяется, является ли данный ряд абсолютно сходящимся. В случае положительного ответа ряд сходится абсолютно. И только в случае, когда ряд из модулей расходится, проверяется, сходится ли исходный ряд условно, например, по Лейбницу.

Пример 20. Исследовать на сходимость ряд .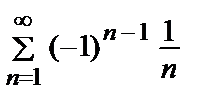

• Ряд знакочередующийсялейбницевского типа. Сходится. Но ряд (гармонический) – расходится. Следовательно, исходный ряд сходится условно.

Пример 21. Исследовать на сходимость ряд 1 – – + – … (два «–», один «+»)

• Ряд сходится абсолютно, т.к. сходится ряд 1 + + + + … (ряд Дирихле (р = 2 > 1))

Утверждение 2. Абсолютно сходящийся ряд при перестановке его членов остается абсолютно сходящимся, и его сумма не изменяется.

Утверждение 3. Если ряд сходится условно, то каково бы ни было число А, можно так переставить члены этого ряда, что преобразованный ряд будет иметь своей суммой число А.

Пример 22. Рассмотрим условно сходящийся ряд 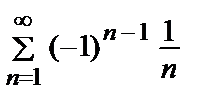= 1 – + – + – …

Обозначим сумму этого ряда через S. Переставим члены ряда так, чтобы за каждым положительным членом следовало два очередных отрицательных: 1 – – + – – + – – 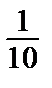…. Покажем, что он сходится и его сумма равна S.

• Рассмотрим последовательность частичных сумм полученного ряда { }:

= 1 – – = – = .

= + = + = + = .

............................................................

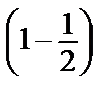Нетрудно убедиться в том, что эта последовательность сходится к S.

А из того, что = – и = – – получаем, что 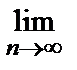существует и равен

S.Т.о., при указанной перестановке членов ряда, получается сходящийся ряд, сумма которого в два раза меньше суммы исходного ряда.

Контрольные вопросы

1. Верно ли, что

а) если ряд абсолютно сходится, то оно сходится и условно? Нет.

б) если ряд сходится условно, то он не сходится абсолютно? Да.

2. Верно ли, что если знакочередующийся ряд сходится, то a_n → 0 (n → ∞) монотонно? Нет.

3. Верно ли для знакочередующегося ряда,что

а) если последовательность { a_n } монотонна (n → ∞), то ряд сходится;Нет.

б) если a_n → 0 (n → ∞), то ряд сходится;Нет.

в) если a_n → 0 (n → ∞) монотонно, то ряд сходится условно;Нет.

г) если a_n → 0 (n → ∞) монотонно, то ряд сходится? Да.

4. Если ряд сходится условно, что можно сказать о сходимости ряда из его положительных

членов?Расходится.

ФУНКЦИОНАЛЬНЫЕ РЯДЫ

Область сходимости

Ряд

f ₁(x) + f ₂(x) + … + f_n (x) + … = ,

членами которого являются функции f_n (x), n = 1, 2, …, определенные на некотором множестве Е числовой оси, называется функциональным рядом.

Например, члены ряда 1 + х + х ² + … определены на интервале –∞ < x < +∞, а члены ряда

1 + arcsin х + arcsin² x + … определены на отрезке –1 ≤ x ≤1.

Функциональный ряд называется сходящимся в точке х ₀ Е, если сходится числовой ряд . Если ряд сходится в каждой точке х ₀ D E и расходится в каждой точке у 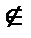D, то говорят, что ряд сходится на множестве D, и называют D областью сходимости этого ряда.

Ряд называется абсолютно сходящимся на множестве D, если на этом множестве сходится ряд .

Областьсходимости некоторых функциональных рядов можно найти с помощью известных достаточных признаков для рядов с положительными членами (Коши, Даламбера).

Пример 23. Найти область сходимости ряда .

• Т.к. числовой ряд сходится при р > 1, то, полагая р =lg x, получим данный ряд, который будет

сходиться при lg x > 1, т.е. прих > 10, и расходиться при lg x ≤ 1, т.е. при 0 < х ≤ 10. Т.о.,

областью сходимости данного ряда является луч 10 < x < +∞.
Пример 24. Найти область сходимости ряда .

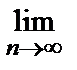
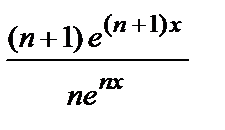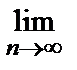
• Рассмотрим ряд = , члены которого положительны при всех значениях х. Применим к нему признак Даламбера. Имеем: λ = = = е^х. При е^х < 1, т.е. прих < 0, этот ряд будетсходиться.Следовательно, исходный ряд сходится абсолютно на интервале

–∞ < х < 0. При x >0 ряд расходится,т.к. λ = е^х > 1. Расходимость ряда при х = 0 очевидна.

Пример 25. Найти область сходимости ряда .

• Члены ряда определены и непрерывны на множестве –∞ < х < +∞. Применяя признак Коши, найдем

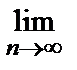
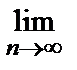
λ = = = +∞ для любого х (–∞, +∞). Следовательно,исходный ряд расходится х.

Признак Вейерштрасса

Пусть для х Ω члены функционального ряда (1) по абсолютной величине не превосходят членов сходящегося числового ряда (2) с положительными членами, т.е.

| f_n (x) | ≤ a_n, n = 1, 2, …, (3) х Ω. Тогда ряд на множестве Ω сходится абсолютно.

⃰ Так как по условию теоремы члены ряда (2) удовлетворяют условию (3) на всем множестве Ω, то по признаку сравнения ряд 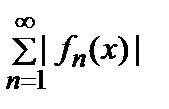сходится при любом х Ω, и,следовательно, ряд (1) сходится на Ω абсолютно.

Пример 25. Исследовать на сходимость ряд .

• Неравенство = ≤ 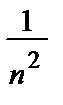выполняется для n = 1, 2, … и для х (–∞, +∞). Числовой ряд сходится. В силу признака Вейерштрасса исходный ряд сходится.

Пример 26. Исследовать на сходимость ряд .

• Члены ряда определены и непрерывны на отрезке [–2,2]. Т.к. = ≥ 0 на отрезке [–2,2] для n = 1, 2, …, то = 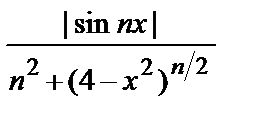≤ ≤ . Т.к.числовой ряд сходится, то попризнаку Вейерштрасса исходный ряд сходится на отрезке [–2,2].