Если существует конечный отличный от нуля предел 
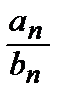 = L, то ряды
= L, то ряды  и
и 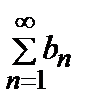 сходятся или расходятся одновременно, т.е. из сходимости одного из них следует сходимость другого и, наоборот, из расходимости одного из них следует расходимость другого.
сходятся или расходятся одновременно, т.е. из сходимости одного из них следует сходимость другого и, наоборот, из расходимости одного из них следует расходимость другого.
⃰ Из существования указанного выше предела следует, что  ε> 0
ε> 0 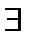 номер Nтакой, что
номер Nтакой, что  n>Nбудет выполняться неравенство
n>Nбудет выполняться неравенство 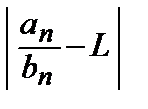 < ε, или L – ε <
< ε, или L – ε < 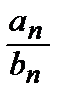 < L + ε. Отсюда (L – ε) bn < аn <(L+ε) bn
< L + ε. Отсюда (L – ε) bn < аn <(L+ε) bn  n>N.
n>N.
Если ряд 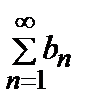 сходится, то сходится и ряд
сходится, то сходится и ряд 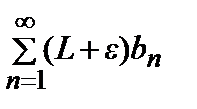 . Но т.к. аn <(L+ε) bn
. Но т.к. аn <(L+ε) bn  n>N, то в силу признака сравнения будет сходиться и ряд
n>N, то в силу признака сравнения будет сходиться и ряд  . Если же ряд
. Если же ряд 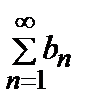 расходится, то расходится и ряд
расходится, то расходится и ряд 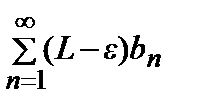 . Т.к.аn >(L–ε) bn
. Т.к.аn >(L–ε) bn  n>N, то в силу признака сравнения будет расходиться и ряд
n>N, то в силу признака сравнения будет расходиться и ряд  .
.
При использовании признаков сравнения для исследования сходимости рядов исходный ряд надо сравнивать с рядом, о котором известно, сходится он или расходится. Такими рядами являются геометрический ряд, гармонический ряд и ряд Дирихле.
Рекомендации:
1. Признаки сравнения обычно используют в случаях, когда другие признаки «не срабатывают».
2. Более распространенным является предельный признак сравнения. При этом часто используют эквивалентность бесконечно малых последовательностей (при n →∞), например,
sin 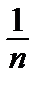 ~ tg
~ tg 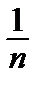 ~ arcsin
~ arcsin 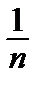 ~ arctg
~ arctg 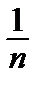 ~ ln
~ ln 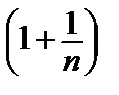 ~
~ 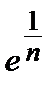 – 1 ~
– 1 ~ 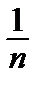 ;
; 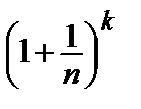 – 1 ~
– 1 ~ 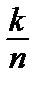 ;
; 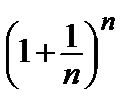 ~ e.
~ e.
3. Признак сравнения обычно используют в случаях, когда в числителе или знаменателе одним из слагаемых является ограниченная функция от n, например, | sin n | ≤ 1, | cos n | ≤ 1, | arctg n | ≤ 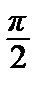 и т.п.
и т.п.
Пример 7. Исследовать на сходимость ряд 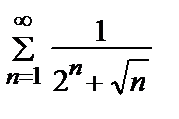 .
.
• НПС: 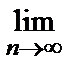 an =
an = 
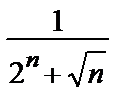 = 0=> может как сходиться, так и расходиться.
= 0=> может как сходиться, так и расходиться.
Признак сравнения:an = 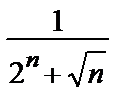 ≤
≤ 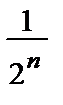 =
= 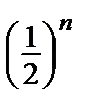 = bn. Ряд
= bn. Ряд 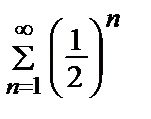 сходящийся геометрический (q =
сходящийся геометрический (q = 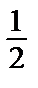 > 1) =>
> 1) =>
сходится исходный (меньший) ряд.
Пример 8. Исследовать на сходимость ряд 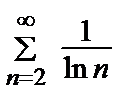 .
.
• НПС: 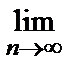 an =
an = 
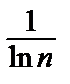 = 0=> может как сходиться, так и расходиться.
= 0=> может как сходиться, так и расходиться.
Признак сравнения:an = 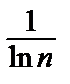 >
> 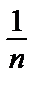 = bn. Ряд
= bn. Ряд 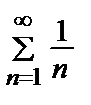 расходящийся гармонический => расходится исходный (больший) ряд.
расходящийся гармонический => расходится исходный (больший) ряд.
Пример 9. Исследовать на сходимость ряд 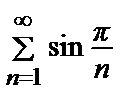 .
.
• НПС: 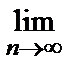 an =
an = 
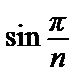 = 0=> может как сходиться, так и расходиться.
= 0=> может как сходиться, так и расходиться.
Предельный признак сравнения:an = 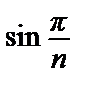 ~
~ 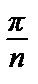 = bn.
= bn. 
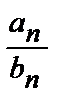 =
= 
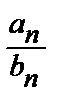 =
= 
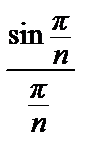 = 1 ≠
= 1 ≠ 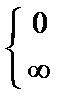 . Т.к. ряд
. Т.к. ряд
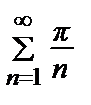 = π
= π 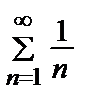 расходящийся(гармонический) => расходится исходный ряд.
расходящийся(гармонический) => расходится исходный ряд.
Признак Даламбера
Пусть дан ряд  , где все аn > 0. Если существует предел
, где все аn > 0. Если существует предел 
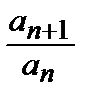 = L, то при 0 ≤ L < 1 ряд сходится, а при L > 1 расходится.
= L, то при 0 ≤ L < 1 ряд сходится, а при L > 1 расходится.
⃰ Пусть существуетпредел 
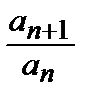 = L, где 0 ≤ L < 1. Возьмем qтакое, что L < q <1. Тогда
= L, где 0 ≤ L < 1. Возьмем qтакое, что L < q <1. Тогда  ε> 0, например, для ε = q–L
ε> 0, например, для ε = q–L 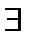 N:
N:  n≥Nвыполняется
n≥Nвыполняется 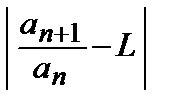 < q–L. В частности,
< q–L. В частности, 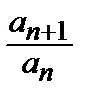 –L < q–Lили
–L < q–Lили 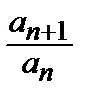 < q. Отсюдаследует, что аn +1< аnq
< q. Отсюдаследует, что аn +1< аnq  n≥N. Из этого неравенства, придавая n последовательно значения N,N +1, N +1, …, получим
n≥N. Из этого неравенства, придавая n последовательно значения N,N +1, N +1, …, получим
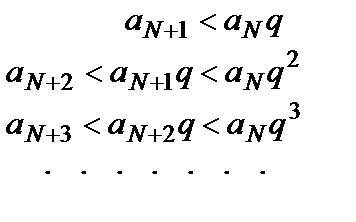
Члены ряды аN+ 1+ аN+ 2+ аN+ 3+ … не превосходят соответствующих членов ряда
аNq + аNq 2+ аNq 3+ …, который сходится как геометрический ряд со знаменателем q, 0 < q < 1. По признаку сравнения ряд аN+ 1+ аN+ 2+ аN+ 3+ … сходится, а, значит, сходится и исходный ряд  .
.
В случаеL > 1, начиная с некоторого номераN,будет выполняться неравенство
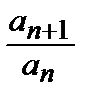 > 1, или аn +1> аn > 0. Следовательно,
> 1, или аn +1> аn > 0. Следовательно,  аn ≠ 0, и ряд
аn ≠ 0, и ряд  расходится, т.к. не выполнен необходимый признак сходимости.
расходится, т.к. не выполнен необходимый признак сходимости.
Замечание. Если 
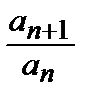 = 1 или не существует, то признак Даламбера ответа о сходимости или
= 1 или не существует, то признак Даламбера ответа о сходимости или
расходимости ряда не дает. Необходимо использовать другие признаки (сравнения, интегральный)
Пример 10. Исследовать на сходимость ряд 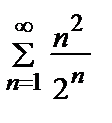 .
.
• НПС: 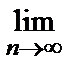 an =
an = 
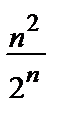
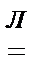
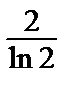

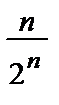
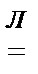
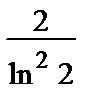

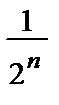 = 0=> может как сходиться, так и расходиться.
= 0=> может как сходиться, так и расходиться.
Д: 
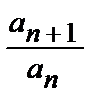 =
= 
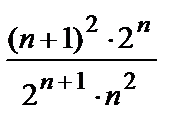 =
= 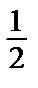

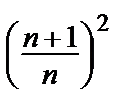 =
= 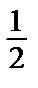

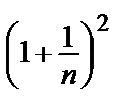 =
= 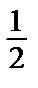 < 1=> исх. ряд сходится.
< 1=> исх. ряд сходится.
Пример 11. Исследовать на сходимость ряд 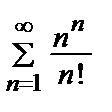 .
.
• НПС: 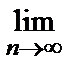 an = ?Может как сходиться, так и расходиться.
an = ?Может как сходиться, так и расходиться.
Д: 
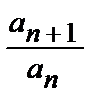 =
= 
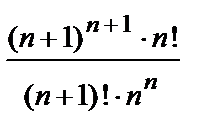 =
= 
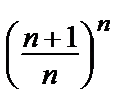 =
= 
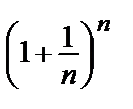 = е > 1=> исх. ряд расходится.
= е > 1=> исх. ряд расходится.
Пример 12. Исследовать на сходимость ряд 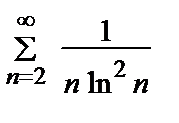 .
.
• НПС: 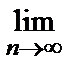 an =
an = 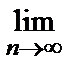
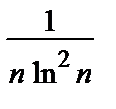 =0. Может как сходиться, так и расходиться.
=0. Может как сходиться, так и расходиться.
Д: 
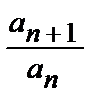 =
= 
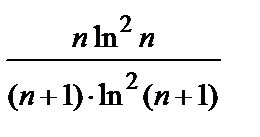 =
= 
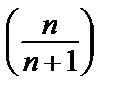
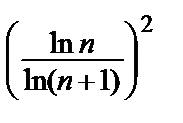 = 1=> надо использовать другой признак.
= 1=> надо использовать другой признак.
Признак Коши
Пусть дан ряд  , где все аn > 0. Если существует предел
, где все аn > 0. Если существует предел 
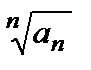 = L, то при 0 ≤ L < 1 ряд сходится, а при L > 1 расходится.
= L, то при 0 ≤ L < 1 ряд сходится, а при L > 1 расходится.
⃰ Пусть L < 1. Возьмем qтакое, что L < q <1. Т.к. существует предел 
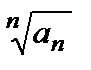 = L, где L < q, то, начиная с некоторого номера N, будет выполняться неравенство
= L, где L < q, то, начиная с некоторого номера N, будет выполняться неравенство 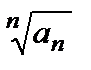 <q.В самом деле, из предельного неравенства вытекает, что
<q.В самом деле, из предельного неравенства вытекает, что  ε> 0, в т.ч.и для ε = q–L
ε> 0, в т.ч.и для ε = q–L 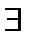 N:
N:  n ≥ N =>
n ≥ N => 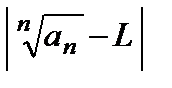 < ε = q– L. Отсюда
< ε = q– L. Отсюда 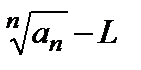 < q–Lили
< q–Lили 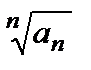 < q => аn < qn
< q => аn < qn  n ≥ N. Т.о.,все члены ряда, начиная с аN+ 1, меньше соответствующих членов сходящегося ряда
n ≥ N. Т.о.,все члены ряда, начиная с аN+ 1, меньше соответствующих членов сходящегося ряда 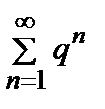 . По признаку сравнения ряд
. По признаку сравнения ряд 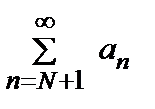 сходится, а, значит, сходится и исходный ряд
сходится, а, значит, сходится и исходный ряд  .
.
В случаеL > 1, начиная с некоторого номераN,  n ≥ N, будет выполняться неравенство
n ≥ N, будет выполняться неравенство
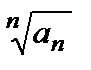 > 1, или аn >1. Следовательно,
> 1, или аn >1. Следовательно,  аn ≠ 0, и ряд
аn ≠ 0, и ряд  расходится, т.к. не выполнен необходимый признак сходимости.
расходится, т.к. не выполнен необходимый признак сходимости.
Замечание. Если L = 1 или не существует, то признак Коши ответа о сходимости или
расходимости ряда не дает. Необходимо использовать другие признаки (сравнения, интегральный)
Пример 13. Исследовать на сходимость ряд 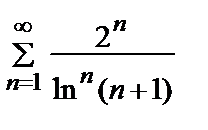 .
.
• НПС: 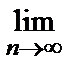 an =?=> может как сходиться, так и расходиться.
an =?=> может как сходиться, так и расходиться.
К: 
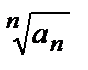 =
= 
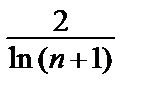 = 0 < 1=> исх. ряд сходится.
= 0 < 1=> исх. ряд сходится.
Пример 14. Исследовать на сходимость ряд 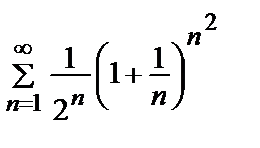 .
.
• НПС: 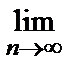 an = ?Может как сходиться, так и расходиться.
an = ?Может как сходиться, так и расходиться.
К: 
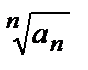 =
= 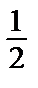

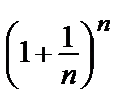 =
= 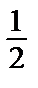 е > 1=> исх. ряд расходится.
е > 1=> исх. ряд расходится.
Интегральный признак
Пусть функция f (x) определена, непрерывна, положительна и не возрастает на луче х ≥ 1. Тогда
1) числовой ряд 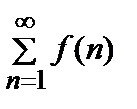 сходится, если сходится несобственный интеграл
сходится, если сходится несобственный интеграл 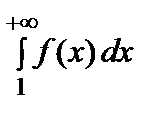 ;
;
2) ряд 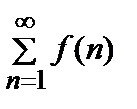 расходится, если расходится несобственный интеграл
расходится, если расходится несобственный интеграл 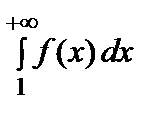 .
.
| f (n) |
| f (3) |
| f (2) |
| f (1) |
| y=f (x) |
| y |
| O |
| x |
| n |
| n-1 |
| 3 |
| 2 |
| 1 |
x 1 = 1, x 2 = 2, x 3 = 3, …, xn = n
и построим две ступенчатые фигуры, состоящие из высту-
пающих и входящихпрямоугольников так, как показано на
рисунке.
Площадь Qкриволинейной трапеции, ограниченной прямыми
х= 1, х= n, y = 0 и кривойу = f (x) равнаQ = 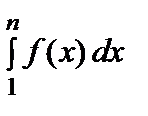 .
.
Возьмем n-ю частичную сумму ряда 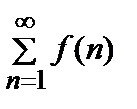 : Sn = f (1) + f (2) + f (3) + … + f (n). Тогда площадь
: Sn = f (1) + f (2) + f (3) + … + f (n). Тогда площадь
Q+ выступающей фигурыбудет равнаQ+ = f (1) + f (2) + f (3) + … + f (n – 1) = Sn- 1, а площадь Q – входящей фигурыравна: Q –= f (2) + f (3) + f (3) + … + f (n) = Sn – f (1).
Из построения и свойств функции f (x) вытекает, что Q – < Q < Q+, т.е.
Sn – f (1) < 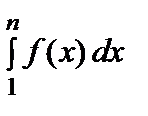 < Sn- 1. Т.к.Sn- 1< Sn (в силу условияf (n)> 0), то
< Sn- 1. Т.к.Sn- 1< Sn (в силу условияf (n)> 0), то
Sn – f (1) < 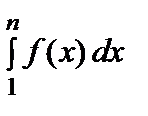 < Sn, n = 1, 2, … (1)
< Sn, n = 1, 2, … (1)
1) Пусть интеграл 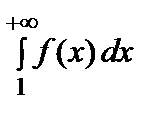 сходится. Тогда существует предел
сходится. Тогда существует предел 
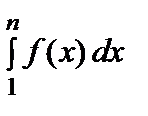 = А. Так как
= А. Так как
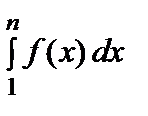 ≤ А =
≤ А = 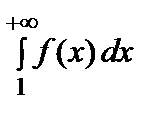 (в силу условияf (х)> 0 для х
(в силу условияf (х)> 0 для х 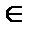 [1, +∞]), то из неравенств (1) следует, что
[1, +∞]), то из неравенств (1) следует, что
Sn < f (1) + 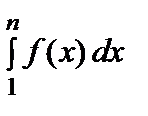 ≤ f (1) + А = М = const, т.е. 0 < Sn < М для n = 1, 2, …. Тем самым, последовательность { Sn } ограничена, и при возрастании n сумма Snвозрастает, т.к.f (n)> 0 для n = 1, 2, …. Поэтому она имеет предел
≤ f (1) + А = М = const, т.е. 0 < Sn < М для n = 1, 2, …. Тем самым, последовательность { Sn } ограничена, и при возрастании n сумма Snвозрастает, т.к.f (n)> 0 для n = 1, 2, …. Поэтому она имеет предел  Sn = S, что означает сходимость ряда
Sn = S, что означает сходимость ряда 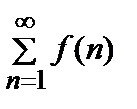 .
.
2) Пусть интеграл 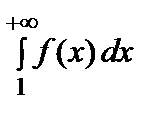 расходится. Т.к. по условию f (х) > 0 для х ≥ 1, то
расходится. Т.к. по условию f (х) > 0 для х ≥ 1, то
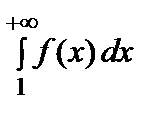 =
= 
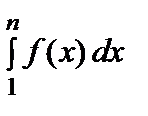 = +∞. Из неравенстваSn ≥
= +∞. Из неравенстваSn ≥ 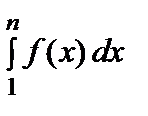 , n = 1, 2, …, следует, что
, n = 1, 2, …, следует, что
 Sn = +∞, т.е.ряд
Sn = +∞, т.е.ряд 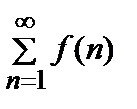 расходится.
расходится.
Пример 15. Исследовать на сходимость ряд 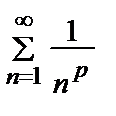 (ряд Дирихле)
(ряд Дирихле)
• НПС: 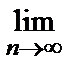 an = 0. Может как сходиться, так и расходиться.
an = 0. Может как сходиться, так и расходиться.
И: 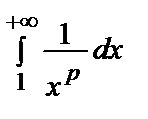 =
= 
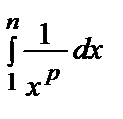 =
= 
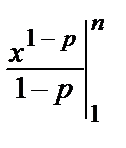 =
= 
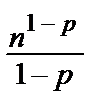 –
– 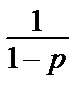 (1)
(1)
1) p > 1 =>(1) = 
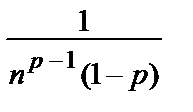 –
– 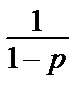 =
= 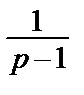 =>интеграл и ряд сходятся и S =
=>интеграл и ряд сходятся и S = 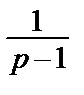 .
.
2) p < 1 =>(1) = 
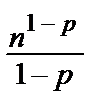 –
– 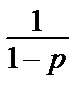 =
= 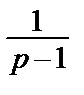 = ∞=>интеграл и ряд расходятся.
= ∞=>интеграл и ряд расходятся.
3) p = 1 =>(1) = 
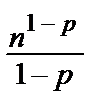 –
– 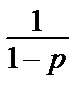 = ∞=>интеграл и ряд расходятся.
= ∞=>интеграл и ряд расходятся.
Пример 16. Исследовать на сходимость ряд 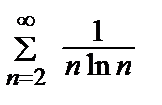 .
.
• НПС: 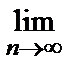 an = 0. Может как сходиться, так и расходиться.
an = 0. Может как сходиться, так и расходиться.
И: 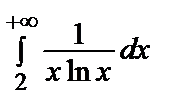 =
= 
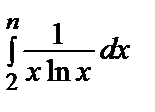 =
= 
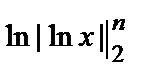 =
=  ln | ln n | – ln | ln 2|= ∞=>интеграл и ряд расходятся.
ln | ln n | – ln | ln 2|= ∞=>интеграл и ряд расходятся.
Пример 17. Исследовать на сходимость ряд 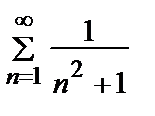 .
.
• НПС: 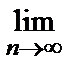 an = 0. Может как сходиться, так и расходиться.
an = 0. Может как сходиться, так и расходиться.
И: 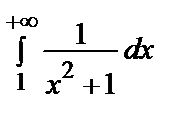 =
= 
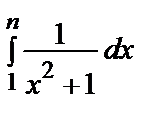 =
= 
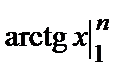 =
= 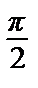 –
– 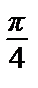 =
= 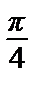 =>интеграл и ряд сходятся и S =
=>интеграл и ряд сходятся и S = 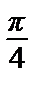 .
.
Контрольные вопросы
1. Можно ли утверждать, что ряд  сходится, если
сходится, если  an = 0? Нет.
an = 0? Нет.
2. Является ли необходимым для сходимости ряда  условие:
условие:
а)  an ≠2;Да.
an ≠2;Да.
б) не все члены ряда равны 2;Да.
в)  an ≠0;Нет.
an ≠0;Нет.
г) не все члены ряда равны 0?Нет.
3. Верно ли что
а) если ряд сходится, то его частичные суммы ограничены;Да.
б) если частичные суммы ряда ограничены, то ряд сходится? Нет. (1 – 1 + 1 – 1 + …)
4. Существует ли ряд, который
а) по признаку Даламбера сходится, а по признаку Коши расходится;Нет.
б) по признаку Коши сходится, а по признаку Даламбера расходится;Нет.
в) по признаку Даламбера расходится, а по интегральному признаку сходится;Нет.
5. Что можно сказать о сходимости ряда 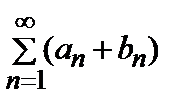 , если
, если
а) ряды  и
и 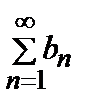 сходятся;Сходится.
сходятся;Сходится.
б) ряды  и
и 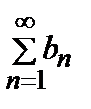 расходятся;Может сходиться или расходиться.
расходятся;Может сходиться или расходиться.
в) ряд  сходится, а ряд
сходится, а ряд 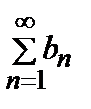 расходятся?Расходится.
расходятся?Расходится.
6. Из того, что ряд 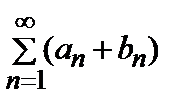 сходится, следует ли, что
сходится, следует ли, что
а) оба ряда  и
и 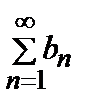 сходятся;Нет.
сходятся;Нет.
б) оба ряда  и
и 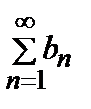 расходятся;Нет.
расходятся;Нет.
в) один из рядов  или
или 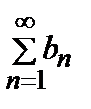 сходится, а другой – расходятся?Нет.
сходится, а другой – расходятся?Нет.
 2018-03-09
2018-03-09 1529
1529
