1. Если все члены функционального ряда  , сходящегося на [ a, b ], умножить на одну и ту же функцию g (x), ограниченную на [ a, b ], то полученный функциональный ряд
, сходящегося на [ a, b ], умножить на одну и ту же функцию g (x), ограниченную на [ a, b ], то полученный функциональный ряд  будет сходиться на [ a, b ].
будет сходиться на [ a, b ].
2. Пусть все члены ряда  , сходящегося на отрезке [ a, b ], непрерывны. Тогда сумма S (x) ряда также непрерывна на этом отрезке.
, сходящегося на отрезке [ a, b ], непрерывны. Тогда сумма S (x) ряда также непрерывна на этом отрезке.
3. Пусть все члены ряда  , сходящегося на отрезке [ a, b ] к функции S (x), непрерывны. Тогда справедливо равенство
, сходящегося на отрезке [ a, b ] к функции S (x), непрерывны. Тогда справедливо равенство  =
=  =
=  , т.е. данный ряд можно почленно интегрировать в пределах от х 0 до х при любых х и х 0 из отрезка [ a, b ].
, т.е. данный ряд можно почленно интегрировать в пределах от х 0 до х при любых х и х 0 из отрезка [ a, b ].
4. Пусть все члены ряда  , сходящегося на отрезке [ a, b ] к функции S (x), имеют непрерывные производные и ряд
, сходящегося на отрезке [ a, b ] к функции S (x), имеют непрерывные производные и ряд  , составленный из этих производных, сходится. Тогда в любой точке х
, составленный из этих производных, сходится. Тогда в любой точке х  [ a, b ] справедливо равенство S´ (x) =
[ a, b ] справедливо равенство S´ (x) =  =
=  , т.е. данный ряд можно почленнодифференцировать.
, т.е. данный ряд можно почленнодифференцировать.
СТЕПЕННЫЕ РЯДЫ
Теорема Абеля
Функциональный ряд вида
c 0 + c 1 x + c 2 x 2 + … + cnxn + … = 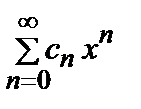 (1)
(1)
или c 0 + c 1(x – x 0) + c 2(x – x 0)2 + … + cn (x – x 0) n + … =  ,(2)
,(2)
где коэффициенты c 0, c 1, c 2, …, cn, … – постоянные, называется степенным рядом.
Ряд (2) заменой x – x 0 на х сводится к ряду (1). Ряд (1) всегда сходится в точке х = 0, а ряд (2) – в
точке x 0, и их сумма в этих точках равна c 0.
| сходится |
| расходится |
| расходится |
| x |
| O |
| x 2 |
| x 1 |
| -x 2 |
| -x 1 |
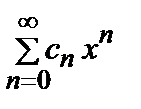 сходится при х = х 1 ≠ 0, то он сходится абсолютно для всех х таких, что | x | < | х 1 |;если степенной ряд расходится при х = х 2, то он расходится при всех х таких, для которых | x | > | х 2 |.
сходится при х = х 1 ≠ 0, то он сходится абсолютно для всех х таких, что | x | < | х 1 |;если степенной ряд расходится при х = х 2, то он расходится при всех х таких, для которых | x | > | х 2 |.
⃰
| x |
| сходится |
| расходится |
| расходится |
| x |
| O |
| R |
| -R |
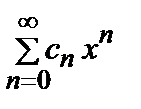 сходится в точке х ≠ 0, то он либо сходится абсолютно в каждой точке числовой прямой, либо найдется число R > 0, такое, что ряд сходится абсолютно при | x | < R и расходится при | x | > R.
сходится в точке х ≠ 0, то он либо сходится абсолютно в каждой точке числовой прямой, либо найдется число R > 0, такое, что ряд сходится абсолютно при | x | < R и расходится при | x | > R.
⃰
Интервал (– R, R) называется интервалом сходимости, а число R радиусом сходимости степенного ряда. Ряд  имеет тот же радиус сходимости, что и ряд
имеет тот же радиус сходимости, что и ряд 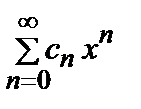 , но его интервал сходимости (x 0 – R, x 0 + R).
, но его интервал сходимости (x 0 – R, x 0 + R).
В точках х = – R и х = R для ряда (1) и х = x 0 – R и х = x 0 + R для ряда (2) получаем числовой ряд, сходимость которого проверяется с помощью признаков сходимости числовых рядов.
Радиус сходимости степенного ряда 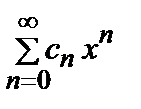 (или ряда
(или ряда  ) можно найти по формулам:
) можно найти по формулам:
R = 
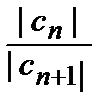 или R =
или R = 
 .
.
⃰ Доказательство для ряда 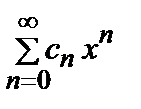 :
:
Для признака Даламбера:

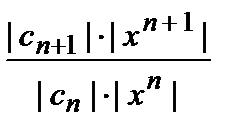 = | x |·
= | x |· 
 < 1 => | x | <
< 1 => | x | < 
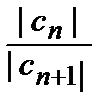 => R =
=> R = 
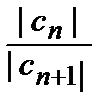 .
.
Для признака Коши:

 = | x |·
= | x |· 
 < 1 => | x | <
< 1 => | x | < 
 => R =
=> R = 
 .
.
Пример 27. Найти область сходимости степенного ряда  .
.
• Имеем: cn = (–1) n– 1 n, cn +1 = (–1) n (n +1). R = 
 =
= 
 = 1 => ряд сходится абсолютнона интервале –1 < x < 1.
= 1 => ряд сходится абсолютнона интервале –1 < x < 1.
Исследуем сходимость ряда на концах интервала сходимости:
При х = –1 получим числовой ряд  =
=  =
=  . Этот ряд расходится,
. Этот ряд расходится,
т.к. не выполняется необходимый признак сходимости  (– n)≠ 0.
(– n)≠ 0.
При х = 1 получим числовой ряд  . Этот ряд расходится, т.к. не выполняется
. Этот ряд расходится, т.к. не выполняется
необходимый признак сходимости  (–1) n– 1 nне существует.
(–1) n– 1 nне существует.
Т.о., областью сходимости данного ряда является интервал –1 < x < 1.
Пример 28. Найти область сходимости ряда  .
.
• Имеем: cn =  , cn +1 =
, cn +1 = 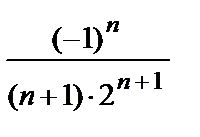 . R =
. R = 
 =
= 
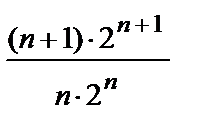 = 2
= 2  = 2 => ряд сходится абсолютнона интервале | x + 2 |<2 или –4 < x < 0.
= 2 => ряд сходится абсолютнона интервале | x + 2 |<2 или –4 < x < 0.
Исследуем сходимость ряда на концах интервала сходимости:
При х = –4 получим числовой ряд  =
=  = –
= –  , который расходится
, который расходится
(гармонический ряд).
При х = 0 получим числовой ряд  =
= 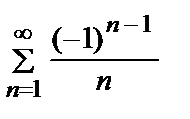 . Это ряд лейбницевского типа =>
. Это ряд лейбницевского типа =>
сходится условно.
Т.о., областью сходимости данного ряда является интервал –4< x ≤0.
Пример 29. Найти область сходимости ряда  .
.
• Имеем: cn =  . R =
. R = 
 =
= 
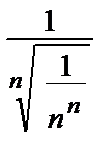 =
=  n = +∞ => ряд сходится абсолютнопри всех значениях х, т.е. область сходимости данного ряда –∞< x ≤ +∞.
n = +∞ => ряд сходится абсолютнопри всех значениях х, т.е. область сходимости данного ряда –∞< x ≤ +∞.
Пример 30. Найти интервал сходимости ряда  .
.
• Имеем: cn = n!, cn +1 = (n +1)!, R = 
 =
= 
 =
= 
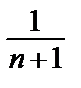 = 0 => РавенствоR =0 означает, что ряд сходится только в точке х = 0, т.е. область сходимости данного ряда состоит из одной точки х = 0.
= 0 => РавенствоR =0 означает, что ряд сходится только в точке х = 0, т.е. область сходимости данного ряда состоит из одной точки х = 0.
 2018-03-09
2018-03-09 188
188








