РЯДЫ Лекции
ЧИСЛОВЫЕ РЯДЫ
Числовой ряд. Сумма ряда
Пусть имеется бесконечная числовая последовательность { аn } = а 1, а 2, а 3, …, аn, …. Просуммируем
члены этой последовательности
а 1 + а 2 + а 3 + … + аn + … =  (1)
(1)
Сумма (1) называется числовым рядом, числа а 1, а 2, а 3, …, аn, … – членами ряда, число аn – общим
(n -м) членом ряда.
Конечная сумма Sn = а 1 + а 2 + а 3 + … + аn =  называется n - й частичной суммой ряда. Частичные суммы ряда образуют свою последовательность{ Sn }:
называется n - й частичной суммой ряда. Частичные суммы ряда образуют свою последовательность{ Sn }:
S 1 = а 1, S 2 = а 1 + а 2, …, Sn = а 1 + а 2 + а 3 + … + аn.
Определение: Если последовательность частичных сумм { Sn } имеет конечный предел  Sn = S, т.е. последовательность { Sn } сходится при n → ∞, то этот предел называют суммой ряда
Sn = S, т.е. последовательность { Sn } сходится при n → ∞, то этот предел называют суммой ряда  , пишут
, пишут
 = S и говорят, что ряд сходится. Если же предел
= S и говорят, что ряд сходится. Если же предел  Sn не существует, то говорят, что ряд
Sn не существует, то говорят, что ряд  расходится (и суммы не имеет).
расходится (и суммы не имеет).
Пример 1. Показать, что ряд  +
+  + … +
+ … +  +… =
+… =  сходится и найти его сумму.
сходится и найти его сумму.
• Имеем:  =
=  =
= 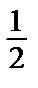
 . Отсюда
. Отсюда
Sn =  +
+  + … +
+ … +  =
= 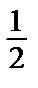
 +
+ 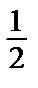
 + … +
+ … + 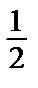
 =
= 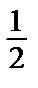
 .
.
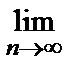 Sn =
Sn = 
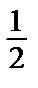
 =
= 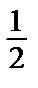 . Т.о., ряд
. Т.о., ряд  сходится и его сумма равнаS =
сходится и его сумма равнаS = 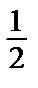 .
.
Пример 2. Исследовать на сходимость ряд из членов геометрической прогрессии со знаменателем q (q ≠ 0),
a + aq + aq 2 + … aqn -1 + …
• Имеем:Sn = a + aq + aq 2 + … aqn -1 =  =
=  –
– 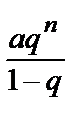 (q ≠ 1).
(q ≠ 1).
Если | q | < 1, то  qn = 0 и
qn = 0 и 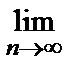 Sn =
Sn =  , т.е., данный ряд сходится и его сумма равна
, т.е., данный ряд сходится и его сумма равна  =
=  .
.
Если | q | > 1, то  qn = ∞ и
qn = ∞ и 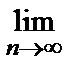 Sn =∞, т.е., ряд расходится.
Sn =∞, т.е., ряд расходится.
Если q = –1, получим расходящийся ряд а – а + а – а + …. Для него 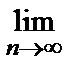 Snне существует.
Snне существует.
Если q = 1, получим ряд а + а + а + а + …. Для него 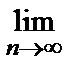 Sn =
Sn = 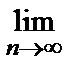 na =∞, т.е.,ряд расходится.
na =∞, т.е.,ряд расходится.
Т.о., рядa + aq + aq 2 + … aqn -1 + … сходится при| q | < 1 и его сумма равна  , и расходится при | q | ≥ 1.
, и расходится при | q | ≥ 1.
Замечательные ряды: (запомнить!)
1). Геометрический ряд – ряд составленный из членов геометрической прогрессии (см. пример 2).
2). Ряд Дирихле  : сходится при p > 1 и расходится при p ≤ 1.
: сходится при p > 1 и расходится при p ≤ 1.
3). Гармонический ряд 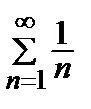 – расходится.
– расходится.
Простейшие действия над рядами
Теорема 1. Если ряд  сходится, то сходится и ряд, полученный из него изменением (в частности отбрасыванием) любого конечного числа его членов. Обратно, из сходимости ряда, полученного из ряда
сходится, то сходится и ряд, полученный из него изменением (в частности отбрасыванием) любого конечного числа его членов. Обратно, из сходимости ряда, полученного из ряда  изменением (в частности отбрасыванием) конечного числа членов, вытекает и его сходимость.
изменением (в частности отбрасыванием) конечного числа членов, вытекает и его сходимость.
⃰ Доказательство следует из конечности суммы конечного числа членов ряда.
Теорема 2. Если ряд  сходится, то сходится и ряд
сходится, то сходится и ряд 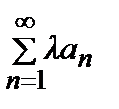 , причем
, причем  = λ
= λ  .
.
⃰ Доказательство следует из того, что  λSn = λ
λSn = λ  Sn.
Sn.
Теорема 3. Если ряды  и
и 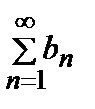 сходится, то их сумма и разность, т.е. ряды
сходится, то их сумма и разность, т.е. ряды 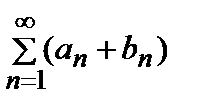 и
и  , также сходятся, причем
, также сходятся, причем 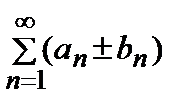 =
=  ±
± 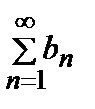 .
.
⃰ Доказательство следует из того, что  (Sn ± Сn) =
(Sn ± Сn) =  Sn ±
Sn ±  Сn.
Сn.
Определение: Если в сходящемся ряде а 1 + а 2 + а 3 + … + аn + аn +1 + аn +2 + … =  отбросить первые n членов, то получим сходящийся ряд аn +1 + аn +2 + … + аn + k + …, который называют n-м остатком этого ряда и обозначают Rn =
отбросить первые n членов, то получим сходящийся ряд аn +1 + аn +2 + … + аn + k + …, который называют n-м остатком этого ряда и обозначают Rn =  . Тогда исходный ряд можно записать
. Тогда исходный ряд можно записать  = Sn + Rn.
= Sn + Rn.
Если S – сумма ряда  , то остаток ряда Rn = S – Sn для любого n = 1, 2, ….
, то остаток ряда Rn = S – Sn для любого n = 1, 2, ….
Пример 3. n-м остатком ряда  является рядRn = aqn + aqn +1 + … + aqn+ k -1 + … =
является рядRn = aqn + aqn +1 + … + aqn+ k -1 + … =  , который
, который
сходится | q | < 1.
 2018-03-09
2018-03-09 389
389







