Приближенное вычисление значений функции

Пусть требуется вычислить значение функции f (x) при х = х ₁ с заданной точностью ε > 0. Если функцию f (x) в интервале (– R, R) можно разложить в степенной ряд

f (x)= c ₀ + c ₁ x + c ₂ x ² + … + c_nxⁿ + …

и х ₁ 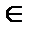(– R, R), то точное значение f (х ₁) равно сумме этого ряда при х = х ₁, т.е.

f (х ₁) = c ₀ + c ₁ х ₁ + c ₂ х ₁² + … + c_nх ₁ ⁿ + …,

 а приближенное – частичной сумме S_n (х ₁), т.е.

f (х ₁) ≈ c ₀ + c ₁ х ₁ + c ₂ х ₁² + … + c_n х ₁ ⁿ.

Точность этого равенства увеличивается с ростом n. Абсолютная погрешность этого приближения равна модулю остатка ряда, т.е. | f (х ₁) – S_n (х ₁) | = | r_n (х ₁) |, где r_n (х ₁) = c_{n +1} х ₁ ^{n +1} + c_{n +2} х ₁ ^{n +2} + ….

Т.о., ошибку | f (х ₁) – S_n (х ₁) | можно найти, оценив остаток r_n (х ₁) ряда. Для рядов лейбницевского типа (см. теорему Лейбница для знакочередующихся рядов) этот остаток не превосходит его первого члена:

| r_n (х ₁) |≤| c_{n +1} х ₁ ^{n +1}|. В остальных случаях составляют ряд из модулей членов ряда и для него стараются подобрать мажорирующий его сходящийся ряд (обычно геометрическую прогрессию), который легко бы суммировался. И в качестве оценки | r_n (х ₁) | берут величину остатка этого нового ряда.

Пример 35. Найти sin1 с точностью до 0,001.

• Имеем: sin х = 1 – +  –  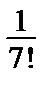+ …, –∞ < х <∞– ряд лейбницевского типа.

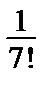Т.к. ≈ 0,008(3) > 0,001, а ≈ 0,0002 < 0,001, то для нахождения sin1 с точностью до 0,001 достаточно первых трех слагаемых sin1≈1 – + = 0,842. Допускаемая при этом ошибка меньше, чем первый отброшенный член, т.е. меньше, чем 0,0002.

Пример 36. Вычислить число е с точностью до 0,001.

• Имеем: е = 1 + + +  + …, –∞ < х <∞.

Оценим ошибку r_n (х):

r_n (х) = + +  + … = < =

= · = , т.е.r_n (х) < .

Остается подобрать наименьшее натуральное число n, чтобы выполнялось неравенство < 0,001. Легко проверить, что оно выполняется приn ≥6. Поэтому имеем:

е ≈1 + + + + + + = 2,718.