Разложение в ряд Маклорена элементарных функций

1) e^x = 1 + 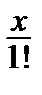+ + 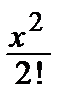… + + …  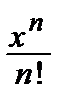(–∞ < x < ∞);

2) e ^{– x} = 1 – 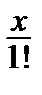+ 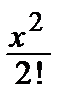– 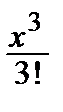+ … +(–1) ⁿ 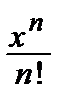+ …  (–∞ < x < ∞);

3) sin x = 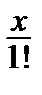– 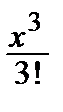+ 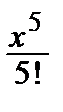– … + (–1) ⁿ 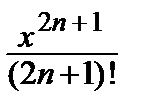+ …  (–∞ < x < ∞);

4) cos x = 1– 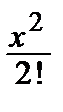+ 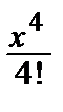– … + (–1) ⁿ 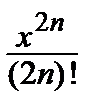+ …  (–∞ < x < ∞);

5)  ln (1 + x) = x – 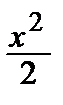+ 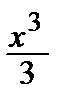– … + (–1) ^{n +1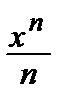} + …  (–1 < x ≤ 1);

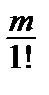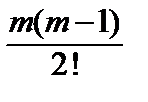6) (1 + x) ^m = 1 + x + x ² + … + 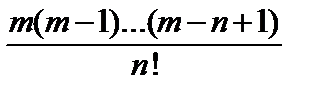xⁿ + …  (–1 < x < 1).

7) 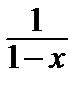 = 1 + x + x ² + … + xⁿ + … (–1 < x < 1).

8) 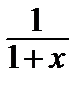 = 1 – x + x ² – x ³ + … + (–1) ⁿxⁿ + … (–1 < x < 1).

9) arctg x = x – 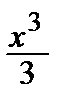+ 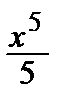– 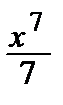+ … + (–1) ⁿ 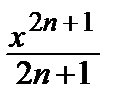+ …  (–1 ≤ x ≤ 1).

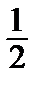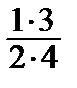
10) arcsin x = x + ·  + + 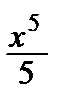…,           –1 < x < 1.

Пользуясь этими разложениями, можно получить разложение в степенной ряд более сложных

функций.

Пример 31. Разложить функцию f (x) = 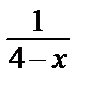в степенной ряд в окрестности точки x ₀ = 2, т.е. по степеням х –2.

• Преобразуем данную функцию 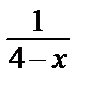= = 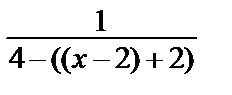= 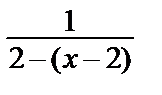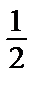· 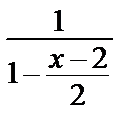=> можно применитьформулу для 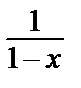, заменив в ней х на :

= · = + + + + …

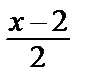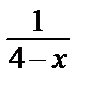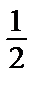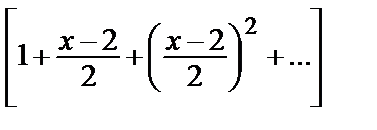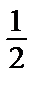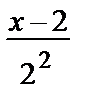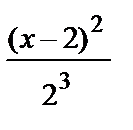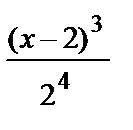Это разложение справедливо, когда выполнено любое из эквивалентных неравенств: 

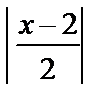< 1 ó| х –2 | < 2 ó–2< х –2< 2 ó 0 < х < 4.    

Пример 32. Разложить функцию f (x) = 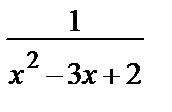 в степенной ряд по степеням х.

• Разложим сначала исходную рациональную функцию на простейшие дроби:

= = – = + .

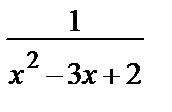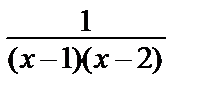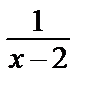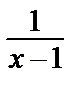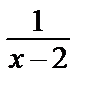Дробь 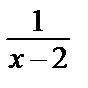 запишем в виде 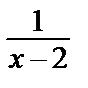= – 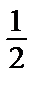· 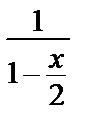=> для каждой из дробе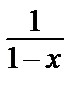й и 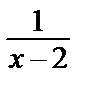можно применить формулу для 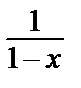, заменив вовторой   х на :

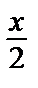Имеем: 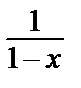= 1 + х + х ² + х ³ 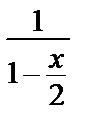+ …                     (1)

= 1 + 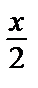 +  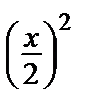+  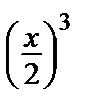+ …             (2)

Ряд (2) сходится для | x | < 1, а ряд (3) для | x | <2 => оба ряда одновременно сходятся для | x | < 1 => в интервале (–1, 1) их можно почленно складывать. В результате получим:

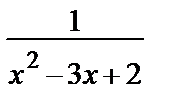=(1+ x + x ²+ x ³+…)– 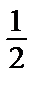· 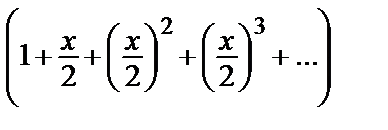= 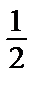+ 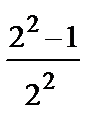· x + 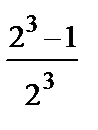· x ² +…+ 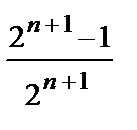· xⁿ +…

Этот ряд сходится абсолютно при | x | < 1.

Пример 33. Применяя почленное интегрирование, вычислить сумму ряда x + 2 x ² + 3 x ³ + 4 x ⁴ + ….

• Имеем: S (x) = x + 2 x ² + 3 x ³ + 4 x ⁴ + … = х (1 + 2 x + 3 x ² + 4 x ³ + …).

Проинтегрируем выражение в скобках: 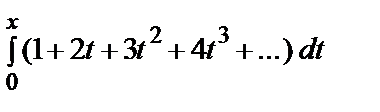 = x + x ² + x ³ + …. Получили бесконечную геометрическую прогрессию со знаменателем х, которая сходится при | x | < 1. Сумма этой прогрессии x + x ² + x ³ + … = .

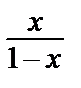   Для нахождения суммы ряда 1 + 2 x + 3 x ² + 4 x ³ + … продифференцируем рядx + x ² + x ³ + … = 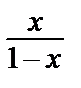и получим:1 + 2 x + 3 x ² + 4 x ³ + … = 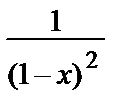. Т.о., получим:

S (x) = x + 2 x ² + 3 x ³ + 4 x ⁴ + … = х (1 + 2 x + 3 x ² + 4 x ³ + …) = х · 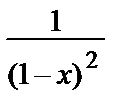= 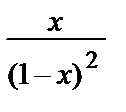, | x | < 1.

Пример 34. Применяя почленноедифференцирование, вычислить сумму ряда x – + – + ….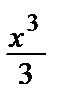

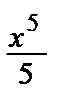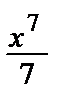• Имеем: S (x)= x – + – + ….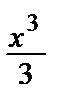

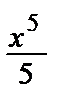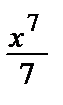Продифференцируем это  выражение: S´ (x)=1 – x ² + x ⁴– x ⁶ + x ⁸ – ….

Получили бесконечную геометрическую прогрессию со знаменателем – х ², которая сходится при | x | < 1. Сумма этой прогрессии S´ (x)= .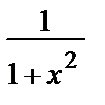

Проинтегрируем это равенство в пределах от 0 до х (x < 1): 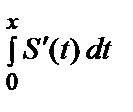= = 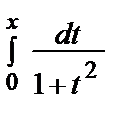arctg x

 

НЕКОТОРЫЕ ПРИЛОЖЕНИЯ СТЕПЕННЫХ РЯДОВ