2018-02-13
2015
С помощью данного алгоритма последовательно проверяется наличие мультиколлинеарности всего массива независимых переменных, каждой независимой переменной с остальными, а также попарная мультиколлинеарность.
В первом случае используется критерий 
(«хи»-квадрат), во втором – 
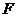-критерий Фишера и в третьем – 
-критерий Стьюдента. Алгоритм распадается на семь шагов.
1-й шаг. Стандартизация (нормализация) данных.
Для каждого наблюдения всех независимых переменных осуществляются расчеты
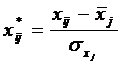. В результате получают векторы нормализованных данных 
, которые образуют матрицу 
.
2-й шаг. Нахождение корреляционной матрицы для независимых переменных.
Вычисляют 
или в матричном виде 
,
где 
– матрица коэффициентов парной корреляции независимых переменных.
3-й шаг. Вычисление значения критерия 
для проверки гипотезы о наличии мультиколлинеарности всего массива данных.
Расчетное значение критерия 
получается из формулы
,
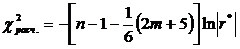где 
– определитель корреляционной матрицы .
Данное значение -критерия сравнивается с табличным 
при числе степеней свободы 
и уровне значимости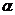 
, где 
– количество независимых переменных.
Если 
, то в массиве данных имеет место мультиколлинеарность.
Следующие два шага позволяют исследовать наличие мультиколлинеарности между каждой независимой переменной и остальными независимыми переменными.
4-й шаг. Нахождение обратной матрицы
.
5-й шаг. Вычисление значений 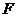-критерия Фишера для проверки гипотезы о наличии мультиколлинеарности между каждой независимой переменной и остальными независимыми переменными.
Для этого используется формула 
, где 
– диагональный элемент матрицы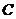 
.
Расчетные значения 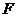-критерия сравниваются с табличными для числа степеней свободы 
и 
, и уровня значимости 
. Если 
, то 
-я переменная мультиколлинеарна с остальными.
Для каждой переменной можно рассчитать коэффициент детерминации
.
Для оценки наличия парной мультиколлинеарности производятся действия, описанные следующими двумя шагами.
6-й шаг. Расчет частных коэффициентов корреляции.
.
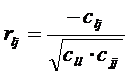Частный коэффициент корреляции показывает тесноту связи между двумя переменными при условии, что остальные переменные постоянны, т.е. не меняются.
7-й шаг. Расчет значений -критерия Стьюдента для каждой пары независимых переменных.
Используется формула 
.
Расчетные значения -критерия сравниваются с табличным знаением при 
степенях свободы и уровне значимости .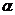
Если 
,то между независимыми переменными 
и 
существует мультиколлинеарность.
