Методы выявления гетероскедастичности

Так как гетероскедастичность принимает различные формы и ее точное проявление в модели почти никогда неизвестно, то и для выявления ее используются различные тесты и методы. Как результат – нет единого универсального метода для оценки данного явления, тем более что ни один из них не доказывает на 100% наличие гетероскедастичности. В литературе по эконометрии приводятся, по меньшей мере, десять различных методов для проверки наличия гетероскедастичности. К их числу относятся: анализ содержания проблемы, графический анализ, тест ранговой корреляции Спирмена, 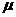-критерий, параметрический и непараметрический тесты Гольдфельда-Квондта, тест Глейсера, тест Парка, тест Бреуша-Пэйгана, тест Уайта и др. Рассмотрим некоторые из них.

15. Критерий 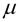обнаружения гетероскедастичности.

М -критерий Используется для проверки гетероскедастичности при большом числе наблюдений исходных данных. Алгоритм метода распадается на пять шагов.

1-й шаг. Все наблюдения зависимой переменной разбиваются на 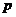групп 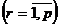в соответствии с уровнем изменения величины .

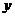2-й шаг. Для каждой группы рассчитываются суммы квадратов отклонений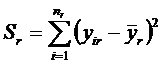

3-й шаг. Находится общая сумма квадратов отклонений по всем группам

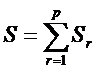
4-й шаг. Вычисляется параметр 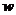по формуле

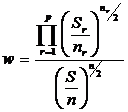где - общее число наблюдений;

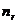- число наблюдений 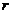-1 группы.

5-й шаг. Рассчитывается значение критерия 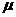по формуле

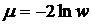который приближенно соответствует критерию при числе степеней свободы 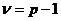, когда дисперсия всех наблюдений однородна.

Если 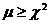при заданном уровне значимости 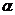, то имеет место гетероскедастичность.

На основе данных из примера, рассмотренного для случая мультиколлинеарности, исследуем наличие гетероскедастичности с помощью 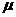-критерия.

Разобьем наблюдения на пять групп по пять наблюдений в каждой группе:

Группа 1	Группа 2	Группа 3	Группа 4	Группа 5
1,82	3,71	3,24	2,83	1,49
2,19	3,07	2,12	3,03	2,69
4,23	1,75	3,95	3,08	2,29
1,66	4,78	2,28	3,49	1,92
1,84	3,35	0,47	2,00	4,22

Найдем сумму квадратов отклонений индивидуальных значений каждой группы от своего среднего значения:

, , , , ,

, ,

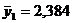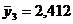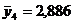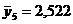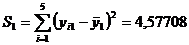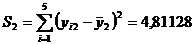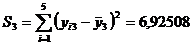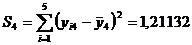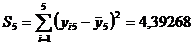Рассчитаем общую сумму квадратов отклонений по пяти группам:

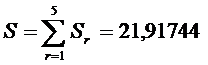Определим параметр :

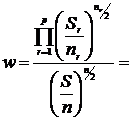
Найдем критерий :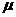

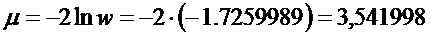Для числа степеней свободы 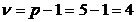и уровня значимости 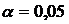находим табличное значение критерия 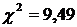и сравниваем с ним полученное значение критерия 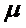. Так как , то делаем заключение об отсутствии гетероскедастичности для исследуемого набора данных.