С тем большей точностью, чем больше n

45Вероятности случайных событий и их свойства

Каждому событию А в схеме случаев приписывается; определенная вероятность , где m - число исходов, благоприятствующих событию А, n - число всех возможных результатов испытания. Таким образом, вероятность Р(A) можно рассматривать как функцию от события А, определенную на поле событий S.

Исходя из определения этой функции может быть установлен ряд ее свойств:

1. Для каждого события А из поля событий S

2. Для достоверного события Ω

3. Если событие А подразделяется на частные случаи Е₁ и Е₂ (А, Е₁, Е₂ ÎS), то имеет место так называемая теорема сложения вероятностей: Р(А) = Р(Е₁) + Р(Е₂).

4. Вероятность события 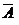, противоположного событию А равна .

Это свойство легко выводится из свойств 2 и 3 так как .

5. Вероятность невозможного события равна нулю.

Р(Æ) = 0

6. Если событие А влечет за собой событие В, (то есть ), то Р(А) ≤ Р(B).

7. Вероятность любого события заключена между нулем и единицей.

0 ≤ Р(А) ≤ 1

Событие А называют практически достоверным, если его вероятность очень близка к единице:

Аналогично, событие А называют практически невозможным, если его вероятность близка к нулю:

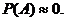
46Биномиальное распределение и его параметры

Формула Бернулли:

О случайной величине числа «успехов» в п испытаниях Бернулли - говорят, что она имеет биномиальное распределение с параметрами п и р.

Покажем, что сумма всевозможных вероятностей , равна единице.

Действительно:

Это соотношение представляет собой формулу бинома Ньютона. Поэтому и вероятностное распределение случайной величины числа «успехов» в п испытаниях Бернулли получило название биномиального распределения.

47Предельная теорема Пуассона

Рассмотрим последовательность схем Бернулли, в каждой из которых число испытаний n постоянно увеличивается (до бесконечности), а вероятность успеха p уменьшается до нуля (в зависимости от n в пределе ), при этом произведение np_n остается практически неизменным (). Как известно в схеме Бернулли вероятность события наступления k успешных испытаний из общего числа n находится по биномиальному закону: .

Теорема Пуассона теперь может быть сформулирована строго следующим образом:

Если так, что (0 < λ < ∞), то

Рассмотрим пример применения Теоремы Пуассона.

Пусть вероятность попадания в цель при каждом выстреле равна р = 0,001. Необходимо найти вероятность редкого события, заключающегося всего в троекратном попадании в цель, если число выстрелов равно п = 5000.

Решение. Считая каждый выстрел за испытание и попадание в цель - за событие УСПЕХ, мы можем для вычисления искомой вероятности воспользоваться теоремой Пуассона:

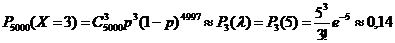. Здесь .

48Классическое определение вероятностей

Классическое определение вероятности сводит понятие вероятности к понятию равновероятности (равновозможности) событий, которое считается основным и не подлежит формальному определению. В общем случае классическое определение вероятности предполагает наличие некоторой полной группы, состоящей из n попарно несовместимых равновозможных элементарных событий:

Е₁, Е₂,..., Е_n (n - количество всех возможных результатов испытания).

На основе событий Е₁, Е₂,..., Е_n и невозможного события Æ, рассмотрением всевозможных сумм событий и противоположных событий, образуем теперь поле событий S. Таким образом, если события А и В принадлежат системе S, то ей принадлежат также события 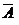, , 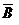АВ, А + В. Кроме того, из определения полноты системы событий следует, что Е ₁+ Е ₂+... + Е _n = Ω и ΩÎS.

Классическое определение вероятности дается только для событий систем, удовлетворяющих описанным выше условиям.

Пусть событие А ÎS и А подразделяется на m частных случаев, входящих в полную группу из n попарно несовместимых равновозможных элементарных событий. Те из возможных элементарных результатов испытания, на которые подразделяется событие А, называются результатами испытания, благоприятствующими событию А. Тогда вероятность Р(A) события А равняется отношению числа m результатов испытания, благоприятствующих событию А, к числу n всех возможных результатов испытания. Таким образом, вероятность Р(A) события А равна:

Таким образом, для применения классического подхода к определению вероятностей должны выполнятся следующие условия.

В результате осуществления случайного опыта (определенного комплексом условий À) может произойти одно из конечного число возможных событий (элементарных исходов)

Е₁, Е₂,..., Е_n.

Элементарных исходов конечное число.

Исходы Е₁, Е₂,..., Е_n несовместны. Они взаимно исключают друг друга, т.е. никакие два из них не могут появиться вместе.

Исходы Е₁, Е₂,..., Е_n образуютполную группу событий. Они исчерпывают собой все возможные результаты опыта, т.е. не может случиться так, что ни один из них не произошел.

События Е₁, Е₂,..., Е_n равновозможны. Условия опыта обеспечивают одинаковую возможность появления каждого из них.

Если исходы (события) Е₁, Е₂,..., Е_n обладают всеми перечисленными свойствами: их конечное число; они несовместимы; образуют полную группу; равновозможны, то эти исходы часто называют случаями, а про опыт говорят, что он сводится к схеме случаев.

49Построение доверительного интервала

Чтобы дать представление о точности и надежности получаемых оценок неизвестных параметров и используются так называемые интервальные оценки или доверительные интервалы.

Пусть для параметра θ по выборочным значениям получена оценка θ*. Возникает необходимость оценить ошибку, совершаемую при использовании полученной оценки.

Назначим некоторую достаточно большую вероятность р (например, р = 0,95). В контексте рассматриваемой задачи эта вероятность называется доверительной вероятностью и обозначается буквой g, так что р = g. Найдем такое значение ε, для которого . Теперь можно утверждать, что вероятность при оценке θ ошибиться больше чем на ε не превысит 1 - γ.

Приведенное выше соотношение можно записать в виде: . А это означает, что с вероятностью γ неизвестное значение параметра θ попадает в интервал .

При этом необходимо отметить одно обстоятельство. Ранее неоднократно рассматривались вероятности попадания случайной величины в заданный неслучайный интервал. Здесь же дело обстоит иначе: величина θ не случайна, зато случаен интервал . Случайно его положение на оси абсцисс, определяемое его центром θ*; случайна вообще и длина интервала 2ε, так как величина ε вычисляется, как правило, по опытным данным. Поэтому в данном случае правильнее толковать величину γ не как вероятность «попадания» точки θ в интервал , а как вероятность того, что случайный интервал накроет точку, соответствующую неизвестному значению θ.

Вероятность γ принято называть доверительной вероятностью, а интервал - доверительным интервалом. Границы интервала ₁ и называются доверительными границами.

Доверительный интервал ‒ это промежуток числовой прямой, который с заранее заданной вероятностью, близкой к единице (доверительной вероятностью), накрывает оцениваемое значение искомого параметра.

50Выборочная совокупность, Вариационный ряд

Предположим, что имеется некоторая случайная величина X, закон распределения которой в точности неизвестен, и требуется: определить этот закон по наблюденным значениям случайной величины или проверить экспериментально - гипотезу о том, что величина X подчинена тому или иному закону. С этой целью над случайной величиной X производится ряд независимых опытов (наблюдений). В каждом из этих опытов случайная величина X принимает определенное значение. Совокупность наблюденных значений величины: 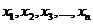и представляет собой первичный статистический материал, подлежащий обработке, осмыслению и анализу.

Такая совокупность называется последовательностью выборочных значений наблюдаемой случайной величины. Для самой случайной величины при этом иногда используется термин «генеральная совокупность». Для совокупности наблюденных значений, кроме того используются термины: выборочная совокупность, случайная выборка или просто выборка. Записывается выборочная совокупность в виде числовой последовательности: 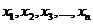. Количество членов последовательности называется объемом выборки.

Простейшей обработкой этой выборки 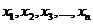, может считаться ее запись в порядке возрастания. Получаемая при этом упорядоченная числовая последовательность называется вариационным рядом.

51Распределение Стьюдента и его основные параметры

Пустьимеется п независимых одинаково распределенных случайных величин Х₁,Х₂,..., Х_n. Каждая из которых распределена по стандартному нормальному закону N(0, 1). Кроме того случайная величинаХ также распределена по стандартному нормальному закону N(0, 1).

Распределением Стьюдента с n (n > 2) степенями свободы называется распределение следующей случайной величиныT _n:

Математическое ожидание и дисперсия случайной величины T _n, имеющей вероятностное распределение Стьюдента с n степенями свободы равны соответственно:

52Статистические гипотезы, критерии их принятия

Под статистической гипотезой понимается всякое высказывание о виде неизвестного распределения, или параметрах известных распределений случайной величины, или о равенстве параметров двух или нескольких распределений, или о независимости выборок, которое можно проверить статистически, то есть, опираясь на результаты наблюдений за случайной величиной.

Наиболее часто формулируются и проверяются гипотезы о числовых значениях одного или нескольких параметров случайной величины (генеральной совокупности), подчиняющейся одному из известных законов распределения, такому, как нормальный, Стьюдента, Фишера и др.

Статистические гипотезы проверяются путем сопоставления (по определенным правилам) выдвинутых предположений с выборочными данными, и по результатам этого сравнения делается вывод о справедливости выдвинутой гипотезы.

Обычно исследование начинается с того, что какая-либо гипотеза, которая из неформальных соображений представляется хорошо согласующейся с ожидаемыми эмпирическими данными объявляется основной (нулевой) и обозначается Н₀. Альтернативная (конкурирующая) гипотеза, утверждающая, что гипотеза Н₀ неверна, обозначается Н₁.

Статистическая гипотеза Н называетсяпростой, если она однозначно определяет распределение случайной величины; в противном случае она называется сложной.

Правило, с помощью которого принимается решение принять или отвергнуть (отклонить) гипотезу Н₀ называется статистическим критерием (решающим правилом).

Если гипотеза Н₀истинна, но статистический критерий ее отвергает, происходит ошибка, которая, называется ошибкой первого рода. Если же гипотеза Н₀принимается в случае, когда она ложна, то говорят, что имеет место ошибка второго рода.

Вероятность ошибки первого рода обозначается a и называется уровнем значимости:

Вероятность ошибки второго рода обозначается

При построении статистического критерия хотелось бы, чтобы обе ошибки a и β были возможно меньше. Но сделать их малыми одновременно невозможно. В такой ситуации более важным является контроль уровня a. Поэтому вероятность a и задается заранее.

Проверку статистических гипотез выполняют на основании наблюдений 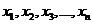(выборки) над случайной величиной X.

53Распределение x² и его основные параметры

Распределения, связанные с нормальным, играют важную роль в теории вероятностей и математической статистике. Рассмотрим их более подробно.

Квадрат стандартной нормально распределенной случайной величины имеет вероятностное распределение χ²(хи квадрат) с одной степенью свободы.

Пусть теперь имеется п независимых одинаково распределенных случайных величин Х₁, Х₂,..., Х_n. Каждая из этих величин распределена по стандартному нормальному закону N(0, 1).

Сумма квадратов этих величин является случайной величиной, вероятностное распределение которой получило название χ²с n степенями свободы или .

Математическое ожидание и дисперсия случайной величины Z _n, имеющей вероятностное распределение χ²с n степенями свободы равны соответственно:

54Способы задания случайных величин

Для того, чтобы задать случайную величину, надо знать те значения, которые она может принимать, и вероятности, с которыми случайная величина принимает свои значения. Любое правило (таблица, функция, график), позволяющее находить вероятности отдельных значений случайной величины или множества этих значений, называется законом распределения случайной величины (или просто распределением). Про случайную величину говорят, что «она подчиняется данному закону распределения».

Закон распределения дискретной случайной величины обычно задается рядом распределения. Так называется таблица, составленная из двух строк: в верхней перечислены все возможные значения случайной величины, а в нижней - соответствующие им вероятности. Очевидно, что сумма всех этих вероятностей равна единице. Эта единица как-то распределена между значениями случайной величины - отсюда и термин «распределение».

Для рассматриваемого примера ряд распределения выглядит следующим образом:

Значения х_i	0	1	2	3
Вероятности p_i	⅛	⅜	⅜	⅛

Закон распределения дискретной случайной величины может быть также задан аналитически, в виде формулы. Для нашего примера аналитическое задание закона распределения случайной величины Х выглядит следующим образом:

Закон распределения дискретной случайной величины может быть также задан графически. Для чего в прямоугольной системе координат строят точки M₁(x₁, p₁), M₂(x₂, p₂),..., M_n(x_n, p_n), где x_i, (значения на оси абсцисс) - возможные значения случайной величины X, а p_i. (значения на оси ординат) - вероятности, соответствующие значениям x_i. Построенные таким образом точки соединяют отрезками прямых. Полученная графическая фигура называется многоугольником распределения или полигоном.

55Теорема Бернулли, сходимость случайных величин по вероятности

Теорема Бернулли. Пусть n_A - частота появления события А в n независимых испытаниях и p есть вероятность наступления события А в каждом из испытаний. Тогда, для любого сколь угодно малого положительного числаε > 0,

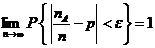Другими словами это утверждение может быть сформулировано так: для любых сколь угодно малых положительных чисел ε и δ найдется такое натуральное число n₀, что для любого n>n₀ будет выполняться неравенство:

Для проверки согласия теоремы Бернулли с опытом было проведено большое число экспериментов. При этом рассматривались события, вероятности которых можно считать по тем или иным соображениям известными, относительно которых легко проводить испытания и обеспечить независимость испытаний, а также постоянство вероятностей в каждом из испытаний. Все подобные опыты дали прекрасное совпадение с теорией.

Говорят, что последовательность сходится почти наверное к случайной величине при , и пишут: п.н., если . Иначе говоря, если при для всех , кроме, возможно, , где 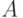- событие, имеющее нулевую вероятность.

Заметим сразу: определение сходимости "почти наверное" требует знания того, как устроены отображения . В задачах же теории вероятностей, как правило, известны не сами случайные величины, а лишь их распределения.

Можем ли мы, обладая только информацией о распределениях, говорить о какой-либо сходимости последовательности случайных величин к случайной величине ?

Можно, скажем, потребовать, чтобы вероятность тех элементарных исходов 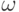, для которых не попадает в " -окрестность" числа , уменьшалась до нуля с ростом . Такая сходимость в функциональном анализе называется сходимостью " по мере", а в теории вероятностей - сходимостью " по вероятности".

56Несмещённость, состоятельность и эффективность статистических оценок

Статистической оценкой Q* неизвестного параметра Q распределения (неизвестного или не полностью известного распределения) случайной величины Х называется функция от наблюденных значений 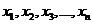этой случайных величин. Неизвестное вероятностное распределение, параметр которого оценивается, часто именуется теоретическим распределением.

Точечной называется статистическая оценка, которая определяется одним числом (некоторая случайная величина.), где 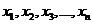результаты наблюдений над случайной величины Х.

Несмещенной называется точечная оценка (являющаяся случайной величиной), математическое ожидание которой равно оцениваемому параметру при любом объеме выборки. Формально это может быть записано следующим образом: .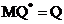

Точечная оценка, математическое ожидание которой не равно оцениваемому параметру, будет называться смещенной оценкой: .

Оценка Q* называется состоятельной, если при увеличении объема выборки n она сходится по вероятности к значению параметра Q.

Несмещенная оценка Q* является эффективной, если ее дисперсия минимальна по отношению к дисперсии любой другой оценки этого параметра.

57Статистический критерий согласия x²

Идите нахуй просто

Статистика c² связана с ситуациями, при которых множество значений рассматриваемой случайной величины X разбито на непересекающиеся подмножества S₁, S₂, … S_r. При этом

Над случайной величиной Xпроизводится n наблюдений, результатом которых является случайная выборка: x₁, x₂, …, x_n. Каждому множеству S_i принадлежат n_i> 0 выборочных значений, и при этом

Рассмотрим следующую статистику (функцию наблюдений):

К.Пирсон доказал, что в пределе при статистика c² имеет вероятностное распределение c² с (r-1) степенью свободы. На практике с достаточной степенью точности уже при n >50 считают, что статистика имеет указанное вероятностное распределение.

Применим полученные результаты к решению конкретной задачи. Пусть имеется дискретная случайная величина Х с известным математическим ожиданием МХ = 3. Над этой случайной величиной производится n наблюдений, результатом которых является случайная выборка: x₁, x₂, …, x_n. Среди этих выборочных значений оказалось n₀-равных либо меньших нуля, n₁-равных 1, и так далее, n_r_-1-равных r-1, и n_r-равных или больших r. Очевидно, что Все эти данные сведены в следующую таблицу:

i	0	1	2	3	4	≥5
n _i	4	13	14	24	16	19

По имеющимся данным необходимо построить статистический критерий проверки гипотезы о том, что случайная величина Х имеет вероятностное распределение Пуассона. Вероятность ошибки первого рода a должна быть равной 0,05.

Для решения задачи используем критерий c²Пирсона. Гипотеза Н₀заключается в том, что случайная величина Х имеет закон распределения Пуассона. Конкурирующая гипотеза Н₁состоит в том, что случайная величина Х имеет закон распределения, отличный от закона Пуассона. Просуммировав значения из второй строки таблицы исходных данных, получим:

Теперь исходя из предположения о справедливости гипотезы Н₀, что случайная величина Х имеет закон распределения Пуассона, вычислим соответствующие значения вероятностей для величины Х по формуле: . Напомним, что по условию задачи λ =MX = 3. Полученные значения запишем в виде третьей строки в исходной таблице:

i	0	1	2	3	4	≥5
n _i	4	13	14	24	16	19
p_i	0,05	0,149	0,224	0,224	0,168	0,185

Следует отметить, что последняя вероятность была вычислена иным образом нежели другие, а именно по следующей формуле: .

Следующим этапом построения статистического критерия является вычисление ожидаемых частот встречаемости конкретных значений случайной величины X в предположении справедливости гипотезы Н₀ при числе испытаний n = 90. Для нахождения ожидаемой частоты встречаемости воспользуемся соотношениями вида: np_i. Найденные таким образом значения оформим в виде четвертой строки нашей таблицы:

i	0	1	2	3	4	≥5
n _i	4	13	14	24	16	19
p_i	0,05	0,149	0,224	0,224	0,168	0,185
np_i	4,48	13,44	20,16	20,16	15,12	16,62

Теперь можно приступить к вычислению критериальной статистики , которая асимптотически распределена по вероятностному распределению c² с пятью степенями свободы. Подставляя в приведенную формулу конкретные значения, получим: .

Для нахождения области принятия гипотезы Н₀по таблицам хи-квадрат распределения отыщем значение квантиля К _a =11,07 (уровня a = 0,05) вероятностного распределения хи-квадрат с 5 степенями свободы. Теперь область принятия гипотезы Н₀будет определятся промежутком: (0; К _a) = (0; 11,07).

Так как значение критериальной статистики c²= 3,07 принадлежит области принятия гипотезы Н₀, то эта гипотеза принимается, то есть считается, что случайная величина Х имеет вероятностное распределение Пуассона.

58Функция плотности нормального закона распределения

Нормальный закон распределения полностью описывается своей функцией плотности вероятностей, которая имеет следующий вид: .

График этой функции имеет симметричную (относительно а) колоколообразную форму. Максимальная ордината кривой графика равная , соответствует точке x = a, являющейся центром симметрии графика. По мере удаления от точки x = a плотность вероятностного распределения падает, и при х → ± ∞ кривая асимптотически приближается к оси абсцисс.

Функция распределения для нормальной случайной величины с параметрами а и σ записывается следующим образом: .

Числовые параметры а и σ, входящие в выражение функции распределения и функции плотности нормального распределения, являются: а - математическим ожиданием, а σ - средним квадратичным отклонением соответствующей случайной величины X. Таким образом:

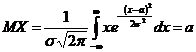Отсюда следует, что нормальное распределение полностью определяется своими математическим ожиданием и дисперсией. В связи с этим следует отметить, что в литературе для нормального распределения часто используется обозначение N(a, σ).

59Априорные и апостериорные вероятности, формула Байеса

Априорная вероятность – это вероятность, присвоенная событию до опыта.

Апостериорная вероятность – это условная вероятность события,полученная в результате опыта.

Имеется полная группа несовместных событий (гипотез) . Вероятности этих гипотез до опыта известны и равны соответственно . Они называются априорными (до опытными) вероятностями. Пусть произведен опыт, в результате которого наблюдено появление некоторого события А. Необходимо найти вероятности , которые называются апостериорными (после опытными) вероятностями. Для нахождения условной вероятности воспользуемся теоремой умножения вероятностей , которая очевидно может быть записана и иным образом: . Отсюда получаем . И далее .

Выражая Р(А) с помощью формулы полной вероятности, окончательно будем иметь:

60Равномерное распределение. Мат ожидание и дисперсия равномерного распределения

Рассмотрим непрерывную случайную величину, о которой известно, что ее возможные значения лежат в некотором определенном интервале, в пределах которого все значения случайной величины одинаково вероятны (точнее, обладают одной и той же плотностью вероятности).

О такой случайной величине говорят, что она распределена по закону равномерной плотности или имеет равномерное распределение.

В общем случае рассмотрим случайную величину X, подчиненную закону равномерной плотности на промежутке числовой оси от а до b, и напишем для нее выражение функции плотности распределения f(х). Очевидно, плотность f(х) постоянна и равна определенному числовому значению с на всем промежутке (а, b) и - нулю вне его. Отсюда следует, что:

Так как по свойству функции плотности площадь, ограниченная кривой ее графика и осью абсцисс, равна единице, то . Отсюда получаем: и для функции плотности f(x):

Выведем теперь выражение для функции распределения F(х) рассматриваемой случайной величины. Для этого воспользуемся известным соотношением между функцией распределения и функцией плотности: