Неравенство и теорема Чебышева

Опыты независимы.

Очевидно, бросание n раз одной и той же монеты есть схема Бернулли с вероятностью успеха р, и вероятностью неудачи q =1-р. Если монета симметрична, то вероятность успеха р = 0,5 и вероятность неудачи q = 1 - р = 0,5.

 

4 Проверка статистических гипотез

Под статистической гипотезой понимается всякое высказывание о виде неизвестного распределения, или параметрах известных распределений случайной величины, или о равенстве параметров двух или нескольких распределений, или о независимости выборок, которое можно проверить статистически, то есть, опираясь на результаты наблюдений за случайной величиной.

Наиболее часто формулируются и проверяются гипотезы о числовых значениях одного или нескольких параметров случайной величины (генеральной совокупности), подчиняющейся одному из известных законов распределения, такому, как нормальный, Стьюдента, Фишера и др.

Статистические гипотезы проверяются путем сопоставления (по определенным правилам) выдвинутых предположений с выборочными данными, и по результатам этого сравнения делается вывод о справедливости выдвинутой гипотезы.

Обычно исследование начинается с того, что какая-либо гипотеза, которая из неформальных соображений представляется хорошо согласующейся с ожидаемыми эмпирическими данными объявляется основной (нулевой) и обозначается Н₀. Альтернативная (конкурирующая) гипотеза, утверждающая, что гипотеза Н₀ неверна, обозначается Н₁.

Статистическая гипотеза Н называетсяпростой, если она однозначно определяет распределение случайной величины; в противном случае она называется сложной.

Правило, с помощью которого принимается решение принять или отвергнуть (отклонить) гипотезу Н₀ называется статистическим критерием (решающим правилом).

Если гипотеза Н₀ истинна, но статистический критерий ее отвергает, происходит ошибка, которая, называется ошибкой первого рода. Если же гипотеза Н₀ принимается в случае, когда она ложна, то говорят, что имеет место ошибка второго рода.

Вероятность ошибки первого рода обозначается a и называется уровнем значимости:

Вероятность ошибки второго рода обозначается

При построении статистического критерия хотелось бы, чтобы обе ошибки a и β были возможно меньше. Но сделать их малыми одновременно невозможно. В такой ситуации более важным является контроль уровня a. Поэтому вероятность a и задается заранее.

Проверку статистических гипотез выполняют на основании наблюдений 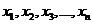 (выборки) над случайной величиной X.

 

5 Доверительный интервал для дисперсии нормального распределения

Как и прежде, имеется нормально распределенная N(a, s) случайная величина Х с неизвестными параметрами. Над этой случайной величиной произведено n независимых испытаний, результаты которых представлены следующей последовательностью: 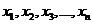. Эта последовательность может понимается, как последовательность случайных величин полностью идентичных случайной величине Х.

По наблюденным значениям 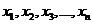 построим статистику χ² (случайную величину, зависящую от наблюдений): .

Может быть доказано, что эта статистика имеет вероятностный закон распределения, который тоже имеет название «χ² - распределение» с (n-1) степенями свободы.

Выберем числовые значения  так, чтобы: .

Напомним, что так определенные числа называются квантилями «χ² - распределения» уровней  соответственно. Теперь становится очевидным следующее соотношение:

, которое может быть преобразовано к следующему виду: .

Остается только преобразовать выражение в скобках, чтобы прийти к окончательному виду:

.

А это и означает, что интервальной оценкой с надежностью γ дисперсии σ² нормально распределенной случайной величины Х является доверительный интервал: .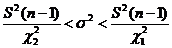

 

 

6 Формула полной вероятности

Рассмотрим случай, когда событие А может произойти в сочетании с одним из m попарно несовместных событий  одно из которых обязательно происходит. Таким образом, объединение этих событий совпадает со всем пространством элементарных исходов:

Поскольку объединение , совпадает со всем пространствомэлементарных исходов, а событие А происходит с одним из H_j, то имеет место очевидное соотношение:

Ввиду попарной несовместности событий правило сложения вероятностейдает:

.

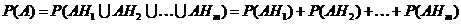Применяя теперь к каждому слагаемому формулу умножения вероятностей, получим так называемую формулу полной вероятности:

.

Краткая запись формулы полной вероятности имеет следующий вид: .

 

7 Закон больших чисел

Математический закон больших чисел является отражением некоторого общего свойства многих реальных процессов.При очень большом числе случайных явлений средний их результат практически перестает быть случайным и может быть предсказан с практической достоверностью. Андрей Николаевич Колмогоров, следующим образом сформулировал его суть. Закон больших чисел - «общий принцип, в силу которого совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая».

Таким образом, закон больших чисел имеет как бы две трактовки. Одна - математическая связанная с конкретными математическими моделями, формулировками, теориями, и вторая - более общая, выходящая за эти рамки. Вторая трактовка связанна с нередко отмечаемым на практике феноменом образования в той или иной степени направленного действия на фоне большого числа скрытых или видимых действующих факторов, внешне такой направленности не имеющих.

Важные теоремы:

Теорема Бернулли. Пусть n_A - частота появления события А в n независимых испытаниях и p есть вероятность наступления события А в каждом из испытаний. Тогда, для любого сколь угодно малого положительного числаε > 0,

.

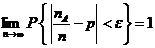Неравенство и теорема Чебышева.

Неравенство Чебышёва. Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине меньше положительного числа ε, не меньше чем :

.

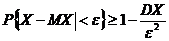Теорема Чебышёва. Если последовательность попарно независимых случайных величин Х₁, Х₂,..., Х_n,... имеет конечные математические ожидания и дисперсии этих величин равномерно ограничены (не превышают постоянного числа С), то среднее арифметическое случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий.

 

8 Статистическое оценивание дисперсии

Если дисперсия случайной величины Х может быть записана следующим образом: , то для эмпирической дисперсии может использоваться соответствующее обозначение:

.

При увеличении числа наблюдений, очевидно, и статистическая дисперсия будет сходиться по вероятности к дисперсии случайной величины Х.

Вот почему и эмпирическая дисперсия принимается за статистическую оценку дисперсии случайной величины Х.

 

9 Центральная предельная теорема

Если случайные величины Х₁, Х₂,..., Х_n,... попарно независимы, одинаково распределены и имеют конечную дисперсию, то при неограниченном увеличении n закон распределения случайной величины неограниченно приближается к нормальному.

 

10 Доверительное оценивание мат ожидания нормально распределённой случайной величины при неизвестной дисперсии.

Таким образом, имеется нормально распределенная N(a, s) случайная величина Х. Над этой случайной величиной производится n независимых испытаний, результаты которых представлены следующей последовательностью: 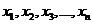. Эта последовательность может пониматься, как последовательность случайных величин полностью идентичных случайной величине Х.

Из этих наблюденных случайных величин сконструируем новую случайную величину T следующего вида:

, здесь, как и ранее .

Оказывается, что случайная величина T имеет распределениеСтьюдента с (n-1) степенями свободы. С учетом ранее введенного обозначения:  случайную величину T можно представить следующим образом: .

Сделаем одно терминологическое замечание. Только что определенная величина Т зависит от наблюдённыхзначений 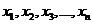, иными словами является функцией от этих значений. В математической статистике любую функцию наблюдений принято называть «статистикой».

Учитывая формальное сходство статистик Ξ и Т и сходство свойств их функций распределений (стандартного нормального и распределения Стьюдента), не должно составить труда получение следующего соотношения:

.

Здесь 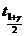 является квантилем распределения Стьюдента c (n-1) степенями свободы.

А это и означает, что интервальной оценкой неизвестного математического ожидания а с доверительной вероятностью γ (для нормально распределенной случайной величины Х при неизвестном стандартном отклонении σ) является доверительный интервал: .

 

 

11 Начальные и центральные моменты случайной величины

Случайные величины называются независимыми, если любое случайное событие, связанное с одной из них не будет зависеть от любого события, определяемого другой случайной величиной.

Начальным моментом порядка к случайной величины X называется величина МХ^k = М(Х^k), которая обозначается следующим образом: ν_k = МХ^k. При этом математическое ожидание является, очевидно, момент первого порядка.

Величина М(Х - МХ)^k называется центральным моментом порядка k и обозначается так: μ_k = М(Х - МХ)^k. Очевидно, дисперсия является центральным моментом второго порядка.

 

12 Дисперсия случайной величины и её свойства

Случайные величины называются независимыми, если любое случайное событие, связанное с одной из них не будет зависеть от любого события, определяемого другой случайной величиной.

Дисперсия случайной величины Х обозначается как DX или D(X). Для вычисления дисперсии из каждого возможного значения вычитается математическое ожидание, полученное отклонение возводится в квадрат, умножается на вероятность соответствующего значения, и все такие произведения суммируются. Описанная процедура означает, что дисперсия есть математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

.

 

1. Дисперсия постоянной величины С равна нулю:

DС = 0.

2. Постоянный множитель можно выносить из-под знака дисперсии случайной величины, предварительно возведя его в квадрат:

D(СХ) =С2D(Х).

3. Дисперсия суммы независимых случайных величин X и Y равна сумме их дисперсий:

D(Х + Y) = DX + DY.

 

13 Эмпирическая ф-я распределения

Эмпирической функцией распределения случайной величины X называется относительная частота события {X < х } в данной выборке: .

Для того чтобы найти значение статистической функции распределения при данном х, достаточно подсчитать число опытов, в которых величина X приняла значение, меньшее чем х, и разделить на объем выборки.

 

14 Мат ожидание случайной величины

Случайные величины называются независимыми, если любое случайное событие, связанное с одной из них не будет зависеть от любого события, определяемого другой случайной величиной.

1. Математическое ожидание постоянной величины С равно самой постоянной:

МС = С.

2. Постоянный множитель можно выносить из-под знака математического ожидания:

М(СХ) =СМ(Х).

3. Математическое ожидание суммы случайных величин X и Y равно сумме математических ожиданий, случаемых:

M(Х + Y) = MX + MY.

4. Математическое ожидание произведения независимых случайных величин X и Y равно произведению их математических ожиданий:

M(ХY) = MX·MY.

 

15 Ф-я распределения и её свойства

Закон распределения дискретной случайной величины может быть задан функцией распределения. Функцией распределения случайной величины X называется функция F (х), выражающая вероятность того, что случайная величина X примет значение, меньшее, чем х. Из данного определения следует, что:

Для рассмотренной выше случайной величины X - числа гербов, выпавших в трех бросаниях симметричной монеты, функция распределения представляется следующим образом:

Функция распределения является универсальной характеристикой случайных величин. Из всех описанных способов задания случайных величин для описания непрерывных случайных величин годится только способ, основанный на рассмотрении функции распределения.

общие свойства функции распределения.

1. Функция распределения F(х) на всей области определения есть неубывающая функция своего аргумента, то есть из неравенства при х₁< х₂ следует F(х₁) ≤ Р(х₂).

2. Предел функция распределения при стремлении х к минус бесконечности равен нулю: .

3. Предел функция распределения при стремлении х к плюс бесконечности равен единице: .

 

16 Доверительное оценивание параметров распределения

В ряде случаев, не удовлетворяясь нахождением точечной оценки некоторого параметра распределения случайной величины, бывает необходимо знать, к каким ошибкам может привести замена неизвестного параметра его точечной оценкой и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы.

Такого рода задачи особенно актуальны при малом числе наблюдений над случайной величиной. При этом сама точечная оценка в значительной мере случайна и замена этой оценкой неизвестного значения параметра может привести к серьезным ошибкам.

Чтобы дать представление о точности и надежности получаемых оценок неизвестных параметров и используются так называемые интервальные оценки или доверительные интервалы.

Пусть для параметра θ по выборочным значениям получена оценка θ*. Возникает необходимость оценить ошибку, совершаемую при использовании полученной оценки.

Назначим некоторую достаточно большую вероятность р (например, р = 0,95). В контексте рассматриваемой задачи эта вероятность называется доверительной вероятностью и обозначается буквой g, так что р = g. Найдем такое значение ε, для которого . Теперь можно утверждать, что вероятность при оценке θ ошибиться больше чем на ε не превысит 1 - γ.

Приведенное выше соотношение можно записать в виде: . А это означает, что с вероятностью γ неизвестное значение параметра θ попадает в интервал .

При этом необходимо отметить одно обстоятельство. Ранее неоднократно рассматривались вероятности попадания случайной величины в заданный неслучайный интервал. Здесь же дело обстоит иначе: величина θ не случайна, зато случаен интервал . Случайно его положение на оси абсцисс, определяемое его центром θ*; случайна вообще и длина интервала 2ε, так как величина ε вычисляется, как правило, по опытным данным. Поэтому в данном случае правильнее толковать величину γ не как вероятность «попадания» точки θ в интервал , а как вероятность того, что случайный интервал  накроет точку, соответствующую неизвестному значению θ.

Вероятность γ принято называть доверительной вероятностью, а интервал  - доверительным интервалом. Границы интервала ₁ и  называются доверительными границами.

Доверительный интервал ‒ это промежуток числовой прямой, который с заранее заданной вероятностью, близкой к единице (доверительной вероятностью), накрывает оцениваемое значение искомого параметра.

Другими словами, интервальной называется оценка, которая определяется двумя числовыми значениями θ₁ и θ₂ - концами интервала, покрывающего оцениваемый параметр θ с заданной вероятностью. Так, что θÎ(θ₁, θ₂).

Далее будут рассмотрены часто встречаемые задачи интервального оценивания основных параметров нормально распределенной случайной величины (нормальной выборки).

 

 

17 Вероятности ошибок при принятии статистических гипотез

Если гипотеза Н₀ истинна, но статистический критерий ее отвергает, происходит ошибка, которая, называется ошибкой первого рода. Если же гипотеза Н₀ принимается в случае, когда она ложна, то говорят, что имеет место ошибка второго рода.

Вероятность ошибки первого рода обозначается a и называется уровнем значимости:

Вероятность ошибки второго рода обозначается

При построении статистического критерия хотелось бы, чтобы обе ошибки a и β были возможно меньше. Но сделать их малыми одновременно невозможно. В такой ситуации более важным является контроль уровня a. Поэтому вероятность a и задается заранее.

Проверку статистических гипотез выполняют на основании наблюдений 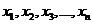 (выборки) над случайной величиной X.

 

18 Локальная предельная теорема Муавра-Лапласа

Локальная теоремаМуавра - Лапласа. Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р (0 < р < 1), то вероятность Р_n(m) того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет соотношению: ,

точность которого, тем выше, чем больше число испытаний n.

Легко усмотреть, что в формулировке теоремы фигурирует функция плотности стандартного нормального распределения: .

 

19 Медиана, квантили и квартили вероятностного распределения

Квантилем, отвечающим заданному уровню вероятности р, называют такое значение x_p случайной величины Х, при котором ее функция распределения принимает значение равное р:

F(x_p) = (X<x_p) = р.

Некоторые квантили имеют особые названия. Так, например, медианой распределения называют квантиль, отвечающий значению вероятности р = ½. Таким образом, медиана делит площадь под графиком функции f(x) плотности случайной величины Х на две равные части.

Квантили, соответствующие значению р = ¼ и р = ¾, называются нижним и верхним квартилями. Если р = 0,9, то x_0,9, для которого F(x_0,9) = (X<x_0,9) = 0,9 называют 90%-ым квантилем.

 

20 Геометрическое распределение и его параметры

закон распределения рассматриваемой дискретной случайной величины X, который может быть записан в виде бесконечного (но счетного) ряда распределения:

 

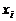	1	2	3	4	......	i	......
					......		......

 

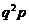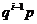Очевидно, вероятности p_i образуют геометрическую прогрессию со знаменателем q = 1 - р, поэтому такое распределение получило название геометрического.

Убедимся теперь в том, что сумма всех вероятностей равна единице.

Теперь могут быть определены основные характеристики - математическое ожидание и дисперсия случайной величины X, распределенной по геометрическому закону. По определению математического ожидания: .

В этой цепочке равенств штрих обозначает производную по переменной q.

Совершенно аналогично, правда несколько сложнее, может быть установлено, что дисперсия случайной величины X, распределенной по геометрическому закону, имеет следующий вид: .

 

21 Ковариация и корреляция двух случайных величин

Напомним, что  и в случае независимости случайных векторов X и Y справедливо равенство , из которого становится очевидным . Таким образом, мы приходим к важному утверждению о том, что: