Корреляционный момент двух независимых случайных величин равен нулю

Если же корреляционный момент не равен нулю, то случайные величины X, Y называются коррелированными. Две коррелированные случайные величины являются зависимыми. Обратное утверждение неверно – две зависимые величины могут быть как коррелированными, так и некоррелированными.

На практике оказывается удобным пользоваться отношением корреляционного момента случайных величин X, Y к корню квадратному из произведения их дисперсий. Это отношение называется коэффициентом корреляции случайных величин X, Y и обозначается

Из свойств матожидания и дисперсии следует, что .

В рассмотренном выше примере, связанным с экспериментом по одновременному бросанию двух симметричных монет случайные величины оказываются зависимыми, так как

.

Коэффициент корреляции этих случайных величин отличен от нуля , а следовательно сами эти величины коррелированы.

 

22 Условные вероятности. Формула Байеса.

Условные вероятности

Допустим, что из общего числа N человек страдает дальтонизмом N_А человек. Все N человек делятся на N₁ женщин и N₂ мужчин, N₁ + N₂ = N. Случайное событие H₁ состоит в том, что наугад выбранный человек является женщиной, а событие H₂ состоит в том, что наугад выбранный человек является мужчиной. Случайное событие А состоит в том, что наугад выбранный человек (мужчина или женщина) страдает дальтонизмом

Для вероятностей (классических) рассмотренных событий имеют место следующие соотношения:

Будем интересоваться дальтонизмом не всех людей, а отдельно дальтонизмом женщин и мужчин. Найдём вероятность того, что наугад выбранная женщина страдает дальтонизмом; очевидно, эта вероятность равна отношению числа женщин, страдающих дальтонизмом, пусть это будет , к общему числу женщин. Для такой вероятности может быть применен символ P(A/H₁), который читается как: "вероятность события А (дальтонизм) при условии, что произошло событие H₁ (выбрана женщина)". Таким образом, могут быть записаны следующие соотношения:

Здесь выражение Р(АН₁) обозначена как раз вероятность произведения (одновременного наступления) событий А и H₁ (случайно выбранная женщина страдает дальтонизмом).

Заметим, что выражение для условной вероятности было получено в предположении применимости классического определения вероятностей (когда все элементарные события равновероятны). Тем не менее, в общем случае условная вероятность определяется аналогичным образом.

Пусть Н - некоторое случайное событие, имеющее ненулевую вероятность, и А - произвольное случайное событие. Условной вероятностью события А при условии Н (при справедливости гипотезы Н) называется величина, определённая соотношением: , где АН представляет собой событие одновременного наступления событий А и Н.

Иногда слова "при условии Н" заменяют словами "если известно, что Н произошло". Условные вероятности остаются неопределёнными, когда гипотеза Н имеет нулевую вероятность.

В противоположность условным вероятностям для большей ясности может использоваться термин безусловная вероятность.

Теоретически, переход от безусловных вероятностей к условным приводит к замене пространства элементарных исходов Ω. на пространство элементарных исходов Н, являющееся частью исходного пространства Ω. Но всякая часть исходного пространства элементарных исходов является его подмножеством, а значит, по определению, случайным событием, которое мы называем Н. Отсюда следует, что все общие теоремы о вероятностях справедливы также и для условных вероятностей. Например, условная вероятность события  противоположного событию А записываются в виде:

 

Имеется полная группа несовместных событий (гипотез) . Вероятности этих гипотез до опыта известны и равны соответственно . Они называются априорными (до опытными) вероятностями. Пусть произведен опыт, в результате которого наблюдено появление некоторого события А. Необходимо найти вероятности, которые называются апостериорными (после опытными) вероятностями. Для нахождения условной вероятности  воспользуемся теоремой умножения вероятностей , которая очевидно может быть записана и иным образом: . Отсюда получаем . И далее .

Выражая Р(А) с помощью формулы полной вероятности, окончательно будем иметь:

.

 

23 Статистические гипотезы. Проверка статистических гипотез

Под статистической гипотезой понимается всякое высказывание о виде неизвестного распределения, или параметрах известных распределений случайной величины, или о равенстве параметров двух или нескольких распределений, или о независимости выборок, которое можно проверить статистически, то есть, опираясь на результаты наблюдений за случайной величиной.

Наиболее часто формулируются и проверяются гипотезы о числовых значениях одного или нескольких параметров случайной величины (генеральной совокупности), подчиняющейся одному из известных законов распределения, такому, как нормальный, Стьюдента, Фишера и др.

Статистические гипотезы проверяются путем сопоставления (по определенным правилам) выдвинутых предположений с выборочными данными, и по результатам этого сравнения делается вывод о справедливости выдвинутой гипотезы.

Обычно исследование начинается с того, что какая-либо гипотеза, которая из неформальных соображений представляется хорошо согласующейся с ожидаемыми эмпирическими данными объявляется основной (нулевой) и обозначается Н₀. Альтернативная (конкурирующая) гипотеза, утверждающая, что гипотеза Н₀ неверна, обозначается Н₁.

Статистическая гипотеза Н называетсяпростой, если она однозначно определяет распределение случайной величины; в противном случае она называется сложной.

Правило, с помощью которого принимается решение принять или отвергнуть (отклонить) гипотезу Н₀ называется статистическим критерием (решающим правилом).

Если гипотеза Н₀ истинна, но статистический критерий ее отвергает, происходит ошибка, которая, называется ошибкой первого рода. Если же гипотеза Н₀ принимается в случае, когда она ложна, то говорят, что имеет место ошибка второго рода.

Вероятность ошибки первого рода обозначается a и называется уровнем значимости:

Вероятность ошибки второго рода обозначается

При построении статистического критерия хотелось бы, чтобы обе ошибки a и β были возможно меньше. Но сделать их малыми одновременно невозможно. В такой ситуации более важным является контроль уровня a. Поэтому вероятность a и задается заранее.

Проверку статистических гипотез выполняют на основании наблюдений 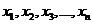 (выборки) над случайной величиной X.

 

24 Теорема и распределение Пуассона

Рассмотрим дискретную случайную величину Х, которая может принимать только целые, неотрицательные числовые значения, причем последовательность этих значений теоретически не ограничена. Говорят, что случайная величина X распределена по закону Пуассона, если вероятность того, что она примет определенное значение k, выражается формулой:

Постоянная λ - это некоторая положительная величина, называемая параметром закона Пуассона.

Убедимся, прежде всего, что последовательность вероятностей, задаваемая формулой приведенной выше, может представлять собой ряд распределения, то есть сумма всех вероятностей равняется единице.

.

Теперь могут быть определены основные характеристики - математическое ожидание и дисперсия случайной величины X, распределенной по закону Пуассона. По определению математического ожидания.

.

Несколько сложнее аналогичным образом устанавливается, что DX = λ. Таким образом, дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию и равна параметру закона Пуассона λ.

Следует отметить особенность распределения Пуассона, связанную с удобствами его использования при значениях вероятностей близких к нулю. В противоположность, биномиальное распределение при очень малых значениях вероятностей использовать крайне неудобно. В связи с этим закон вероятностного распределения Пуассона часто называют законом «редких событий». Оправданием такого названия в определенной степени является приводимое ниже утверждение:

Теорема Пуассона.

Рассмотрим последовательность схем Бернулли, в каждой из которых число испытаний n постоянно увеличивается (до бесконечности), а вероятность успеха p уменьшается до нуля (в зависимости от n в пределе ), при этом произведение np_n остается практически неизменным (). Как известно в схеме Бернулли вероятность события наступления k успешных испытаний из общего числа n находится по биномиальному закону: .

Теорема Пуассона теперь может быть сформулирована строго следующим образом:

Если  так, что (0 < λ < ∞), то

 

25 Правило трёх сигм

Для большинства встречающихся случайных величин с практической достоверностью можно утверждать, что они не отклоняются от своего математического ожидания более чем на 3σ_х.

Уровень доверия этого утверждения зависит от закона распределения случайной величины, но во всех не искусственно придуманных случаях он весьма высок (порядка 90% и выше). Приведённое выше правило носит специальное название «правила трех сигм».

Таким образом, если нам не известен закон распределения случайной величины, но тем или иным способом удалось найти только две числовые характеристики случайной величины - ее математическое ожидание  и стандартное отклонение , то ориентировочное представление о том, в каких пределах лежат ее возможные значения, определяется «правилом трех сигм»:

 

26 Биномиальное распределение

Формула Бернулли:

О случайной величине числа «успехов» в п испытаниях Бернулли - говорят, что она имеет биномиальное распределение с параметрами п и р.

Покажем, что сумма всевозможных вероятностей , равна единице.

Действительно:

Это соотношение представляет собой формулу бинома Ньютона. Поэтому и вероятностное распределение случайной величины числа «успехов» в п испытаниях Бернулли получило название биномиального распределения.

 

27 Статистическое определение вероятности

Пусть производится серия из n одинаковых случайных опытов, относительной частотой (частостью) некоторого события А в этой серии называется отношение числа опытов n_A, в которых это событие произошло, к общему числу произведенных опытов.

Статистической вероятностью Р(А) случайного события А называется относительная частота события А (при большом числе испытаний n):

Несмотря на внешнее сходство полученного выражения с соотношением, используемым в классическом определении вероятности, эти формулы различны по существу.

Формула вычисления вероятности, основанная на классическом подходе, используется для теоретического использования. Для ее применения проведение опытов не требуется. Статистический подход по существу основывается на экспериментах, данные которых и позволяют определить вероятности случайных событий.

 

28 Априорные и апостериорные распределения вероятностей. Формула Байеса

Имеется полная группа несовместных событий (гипотез) . Вероятности этих гипотез до опыта известны и равны соответственно . Они называются априорными (до опытными) вероятностями. Пусть произведен опыт, в результате которого наблюдено появление некоторого события А. Необходимо найти вероятности , которые называются апостериорными (после опытными) вероятностями. Для нахождения условной вероятности  воспользуемся теоремой умножения вероятностей , которая очевидно может быть записана и иным образом: . Отсюда получаем . И далее .

Выражая Р(А) с помощью формулы полной вероятности, окончательно будем иметь:

.

 

 

29 Функция плотности вероятностного распределения и её свойства