Пусть имеется непрерывная случайная величина X с функцией распределения F(х), которая для большинства практических ситуаций обладает свойством непрерывности и дифференцируемости. Вычислим вероятность попадания этой случайной величины на промежуток оси абсцисс от х до х+Δх:
 .
.
Определим отношение этой вероятности к длине промежутка, на котором она сосредоточена.
 .
.
Это будет средняя вероятность, приходящаяся на единицу длины этого промежутка, другими словами - средняя плотность вероятности. Будем теперь уменьшать длину промежутка Δх до нуля, переходя к пределу:
 .
.
В пределе получаем производную от функции распределения, которая обычно обозначается 
С другой стороны, функция распределения F(x) является первообразной для функции плотности f(x) так, что может быть записано следующее соотношение:  .
.
Определенная таким образом функция f(х) характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (или «плотностью вероятности») непрерывной случайной величины X.
основные свойства плотности распределения.
1. Плотность распределения есть неотрицательная функция:

Это свойство непосредственно вытекает из того, что функция распределения F(х) есть неубывающая функция.
2. Интеграл в бесконечных пределах от плотности распределения равен единице:

Это соотношение следует из соотношений:  и
и 
Геометрически основные свойства плотности распределения означают, что вся кривая графика функции плотности распределения лежит не ниже оси абсцисс. Кроме того, полная площадь, ограниченная кривой графика функции плотности распределения и осью абсцисс, равна единице.
30 Полигон и гистограмма
Случайные величины, которые принимают числовые значения, отделенные на числовой оси друг от друга конечными промежутками, называются дискретными случайными величинами.
Закон распределения дискретной случайной величины может быть заданграфически. Для чего в прямоугольной системе координатстроятточки M1(x1, p1), M2(x2, p2),..., Mn(xn, pn), где xi, (значения на оси абсцисс) - возможные значения случайной величины X, а pi. (значения на оси ординат) -вероятности,соответствующиезначениям xi. Построенные таким образом точки соединяют отрезками прямых. Полученная графическая фигура называется многоугольником распределения или полигоном.
Статистический ряд часто оформляется графически в виде так называемой гистограммы. Гистограмма строится следующим образом. По оси абсцисс откладываются интервалы группировки, и на каждом из интервалов как на основании строится прямоугольник, площадь которого равна соответствующей относительной частоте. Для построения гистограммы нужно частоту каждого интервала разделить на его длину и полученное число взять в качестве высоты прямоугольника. Из способа построения гистограммы следует, что полная площадь ее равна единице.

Очевидно, при увеличении объема выборки будет увеличиваться и общее число интервалов группировки, а длины интервалов будут уменьшаться, при этом гистограмма будет все более приближаться к некоторой кривой, ограничивающей площадь равную единице. Нетрудно убедиться, что эта кривая представляет собой график плотности распределения исходной случайной величины Х.
Полигон
Полигон также является графическим представлением статистического ряда. Полигон образуется ломаной линией, отрезки прямых линий которой, соединяют точки координатной плоскости (х, у). Координата х – является центром некоторого интервала группировки, а координата у равна относительной частоте встречаемости значений выборки на данном интервале.

(дополнительно) Случайные величины, которые принимают числовые значения, отделенные на числовой оси друг от друга конечными промежутками, называются дискретными случайными величинами.
Закон распределения дискретной случайной величины может быть заданграфически. Для чего в прямоугольной системе координатстроятточки M1(x1, p1), M2(x2, p2),..., Mn(xn, pn), где xi, (значения на оси абсцисс) - возможные значения случайной величины X, а pi. (значения на оси ординат) -вероятности,соответствующиезначениям xi. Построенные таким образом точки соединяют отрезками прямых. Полученная графическая фигура называется многоугольником распределения или полигоном.
31 Экспоненциальное распределение вероятностей
Плотность показательного распределения имеет вид: 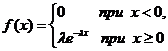 .
.
Здесь λ > 0 постоянный параметр.
Функция распределения экспоненциального закона выражается следующим образом:
 .
.
Для случайной величины, распределенной по экспоненциальному закону математическое ожидание равно:

Дисперсия может быть найдена следующим образом: 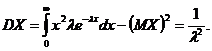
32 Теорема умножения вероятностей
Условные вероятности
Допустим, что из общего числа N человек страдает дальтонизмом NА человек. Все N человек делятся на N1 женщин и N2 мужчин, N1 + N2 = N. Случайное событие H1 состоит в том, что наугад выбранный человек является женщиной, а событие H2 состоит в том, что наугад выбранный человек является мужчиной. Случайное событие А состоит в том, что наугад выбранный человек (мужчина или женщина) страдает дальтонизмом
Для вероятностей (классических) рассмотренных событий имеют место следующие соотношения: 
Будем интересоваться дальтонизмом не всех людей, а отдельно дальтонизмом женщин и мужчин. Найдём вероятность того, что наугад выбранная женщина страдает дальтонизмом; очевидно, эта вероятность равна отношению числа женщин, страдающих дальтонизмом, пусть это будет  , к общему числу женщин. Для такой вероятности может быть применен символ P(A/H1), который читается как: "вероятность события А (дальтонизм) при условии, что произошло событие H1 (выбрана женщина)". Таким образом, могут быть записаны следующие соотношения:
, к общему числу женщин. Для такой вероятности может быть применен символ P(A/H1), который читается как: "вероятность события А (дальтонизм) при условии, что произошло событие H1 (выбрана женщина)". Таким образом, могут быть записаны следующие соотношения:

Здесь выражение Р(АН1) обозначена как раз вероятность произведения (одновременного наступления) событий А и H1 (случайно выбранная женщина страдает дальтонизмом).
Заметим, что выражение для условной вероятности было получено в предположении применимости классического определения вероятностей (когда все элементарные события равновероятны). Тем не менее, в общем случае условная вероятность определяется аналогичным образом.
Пусть Н - некоторое случайное событие, имеющее ненулевую вероятность, и А - произвольное случайное событие. Условной вероятностью события А при условии Н (при справедливости гипотезы Н) называется величина, определённая соотношением:  , где АН представляет собой событие одновременного наступления событий А и Н.
, где АН представляет собой событие одновременного наступления событий А и Н.
Иногда слова "при условии Н" заменяют словами "если известно, что Н произошло". Условные вероятности остаются неопределёнными, когда гипотеза Н имеет нулевую вероятность.
В противоположность условным вероятностям для большей ясности может использоваться термин безусловная вероятность.
Теоретически, переход от безусловных вероятностей к условным приводит к замене пространства элементарных исходов Ω. на пространство элементарных исходов Н, являющееся частью исходного пространства Ω. Но всякая часть исходного пространства элементарных исходов является его подмножеством, а значит, по определению, случайным событием, которое мы называем Н. Отсюда следует, что все общие теоремы о вероятностях справедливы также и для условных вероятностей. Например, условная вероятность события  противоположного событию А записываются в виде:
противоположного событию А записываются в виде: 
Формула  , выражающая значение условной вероятности события А, если известно, что событие Н произошло, может быть представлена в следующем виде:
, выражающая значение условной вероятности события А, если известно, что событие Н произошло, может быть представлена в следующем виде:  . Это соотношение называют формулой (или теоремой) умножения вероятностей.
. Это соотношение называют формулой (или теоремой) умножения вероятностей.
С другой стороны, если  может быть рассмотрено соотношение
может быть рассмотрено соотношение 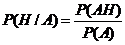 , которое может быть представлено в следующем виде:
, которое может быть представлено в следующем виде: 
Полученную формулу называют теоремой умножения вероятностей для так называемых зависимых событий А и Н. События А и Н могут бытьнезависимыми, если появление одного из них никак не влияет на вероятность появления другого, то есть условная вероятность события А в предположении, что Н произошло, совершенно такая же, как и без этого предположения: Р(А/Н) = Р(А).
Для независимых событий формула умножения вероятностей имеет вид:  . Более того
. Более того  , откуда
, откуда  , то есть события Н и А также независимы.
, то есть события Н и А также независимы.
Свойство независимости событий взаимно, и имеет место и для противоположных событий.
Таким образом, для независимых событий теорема умножения вероятностей формулируется следующим образом: вероятность произведения независимых событий равна произведению их вероятностей.
33 Поле случайных событий
Рассматривается некоторая система S подмножеств множества Ω. Элементы системы S называются случайными событиями. Предполагаются, что для системы S выполняются следующие условия:
1. S в качестве элемента содержит множество Ω. То есть ΩÎS.
2. Если А и В - подмножества множества Ω и входят в S в качестве элементов, то в качестве элементов S содержит также множества 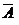 ,
,  , АВ.
, АВ.
При этом под  понимается объединение множеств А и В, то есть множество, составленное из элементов Ω, входящих или в А, или в В, или и в А и в В; под АВ (пересечение множеств А и В) понимаем множество, состоящее из элементов Ω, входящих и в А и в В; и, наконец, под
понимается объединение множеств А и В, то есть множество, составленное из элементов Ω, входящих или в А, или в В, или и в А и в В; под АВ (пересечение множеств А и В) понимаем множество, состоящее из элементов Ω, входящих и в А и в В; и, наконец, под 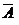 (
(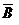 ) - множество элементов Ω, не входящих в А (в В).
) - множество элементов Ω, не входящих в А (в В).
Поскольку в S в качестве элемента входит все множество Ω, то согласно второму требованию S содержит также  , т. е. S в качестве элемента содержит пустое множество Æ.
, т. е. S в качестве элемента содержит пустое множество Æ.
Очевидно, что второе требование влечет за собой принадлежность к множеству S сумм, произведений и дополнений конечного числа событий, принадлежащих S. Таким образом, рассмотренные элементарные операции над случайными событиями не могут вывести за пределы множества случайных событий.
Система событий S, удовлетворяющая приведенным выше условиям, называется полем событий.
34Геометрическое определение вероятностей
Допустим, что на плоскости имеется некоторая область W и в ней содержится другая область w. В область W наудачу бросается точка и спрашивается, чему равна вероятность того, что точка попадет в область w. При этом выражению «точка бросается наудачу в область W» придается следующий смысл: брошенная точка может попасть в любую точку области W, вероятность попасть в какую-либо часть области W пропорциональна площади этой части (либо длине, если рассматриваются области на прямой линии) и не зависит от ее расположения и формы.
Таким образом, по определению, вероятность попадания в область w при бросании наудачу точки в область W определяется следующим образом:

35Аксиоматическое построение теории вероятностей
Изначально постулируется наличие множества (пространства) Ω элементарных событий. Что представляют собой элементы этого множества для логического развития теории вероятностей безразлично. Далее рассматривается некоторая система S подмножеств множества Ω. Элементы системы S называются случайными событиями. Предполагаются, что для системы S выполняются следующие условия:
1. S в качестве элемента содержит множество Ω. То есть ΩÎS.
2. Если А и В - подмножества множества Ω и входят в S в качестве элементов, то в качестве элементов S содержит также множества 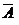 ,
,  , АВ.
, АВ.
При этом под  понимается объединение множеств А и В, то есть множество, составленное из элементов Ω, входящих или в А, или в В, или и в А и в В; под АВ (пересечение множеств А и В) понимаем множество, состоящее из элементов Ω, входящих и в А и в В; и, наконец, под
понимается объединение множеств А и В, то есть множество, составленное из элементов Ω, входящих или в А, или в В, или и в А и в В; под АВ (пересечение множеств А и В) понимаем множество, состоящее из элементов Ω, входящих и в А и в В; и, наконец, под 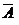 (
(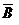 ) - множество элементов Ω, не входящих в А (в В).
) - множество элементов Ω, не входящих в А (в В).
Поскольку в S в качестве элемента входит все множество Ω, то согласно второму требованию S содержит также  , т. е. S в качестве элемента содержит пустое множество Æ.
, т. е. S в качестве элемента содержит пустое множество Æ.
Очевидно, что второе требование влечет за собой принадлежность к множеству S сумм, произведений и дополнений конечного числа событий, принадлежащих S. Таким образом, рассмотренные элементарные операции над случайными событиями не могут вывести за пределы множества случайных событий.
Система событий S, удовлетворяющая приведенным выше условиям, называется полем событий.
При аксиоматическом построении теории вероятностей от поля событий требуется выполнение и следующего условия:
3. Если подмножества А1, А2,.., Аn,... множества Ω являются элементами множества S, то и их бесконечное объединение (сумма) А1 + А2 +...+ Аn +... и бесконечное пересечение (произведение) А1А2... Аn... также являются элементами S.
Множество S, образованное описанным способом, носит название борелевского поля событий.
Изложенный таким образом способ определения случайного события вполне согласуется с представлениями, полученными выше при рассмотрении конкретных примеров.
Естественно вводятся и следующие определения. Если два случайных события А и В не имеют в своем составе одних и тех же элементов множества Ω, то естественно их называть несовместимыми.
Случайное событие Ω называется достоверным событием, а случайное событие Æ (пустое множество) - невозможным событием. События А и 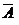 называются противоположными.
называются противоположными.
Аксиоматическое определение вероятностей включает следующие утверждения:
1. Каждому случайному событию А из борелевского поля событий S ставится в соответствие неотрицательное число Р(А), называемое его вероятностью. Иными словами, на множестве S всевозможных событий А вводится функция Р, называемая вероятностной мерой.
2. Р(Ω) = 1.
З. Если события А1, А2,.., Аn,... попарно несовместимы, то
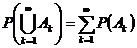
Из перечисленных аксиом может быть получен ряд важных утверждений.
1. Вероятность невозможного события равна нулю. Р(Æ) = 0.
2. Для любого события А вероятность события 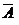 , противоположного событию А равна
, противоположного событию А равна  .
.
3. Вероятность любого события А ÎS заключена между нулем и единицей так, что 0 ≤ Р(А) ≤ 1.
4. Если событие А влечет за собой событие В, (то есть  ), то Р(А) ≤ Р(B).
), то Р(А) ≤ Р(B).
5. Если А1, А2,.., Аn произвольные события из S, то
Р(А1 + А2 +...+ Аn) ≤ Р(А1) + Р(А2) +...+ Р(Аn).
Приведенное аксиоматическое построение вероятности в терминах теории множеств есть не что иное, как введение на множестве Ω нормированной, счетно-аддитивной, неотрицательной меры Р, определенной для всех элементов множества S.
Таким образом при аксиоматическом определении понятия вероятности должно быть указано исходное множество элементарных событий Ω, множество случайных событий S и определенная на S функция Р. Совокупность этих трех составляющих {Ω, S,Р} называется вероятностным пространством.
36Случайные величины и их распределения
Случайной величиной называется величина, которая в результате случайного опыта может принять то или другое значение, заранее неизвестное.Случайные величины, которые принимают числовые значения, отделенные на числовой оси друг от друга конечными промежутками, называются дискретными случайными величинами.
Случайные величины могут относиться и к другому типу. Значения таких случайных величин заполняют некоторый участок числовой оси без промежутков, а сами такие случайные величины называютсянепрерывными
 2018-02-13
2018-02-13 4697
4697
