Закон распределения дискретной случайной величины обычно задается рядом распределения. Так называется таблица, составленная из двух строк: в верхней перечислены все возможные значения случайной величины, а в нижней - соответствующие им вероятности. Очевидно, что сумма всех этих вероятностей равна единице. Эта единица как-то распределена между значениями случайной величины - отсюда и термин «распределение».
37Нормальное вероятностное распределение
Может считаться аналогом закона Пуассона для непрерывных случайных величин. Плотность показательного распределения имеет вид: 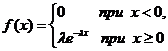 .
.
Здесь λ > 0 постоянный параметр.
Функция распределения экспоненциального закона выражается следующим образом:
 .
.
Для случайной величины, распределенной по экспоненциальному закону математическое ожидание равно:

Дисперсия может быть найдена следующим образом: 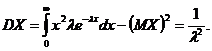
38Независимые случайные величины. Схема Бернулли
Случайные величины называются независимыми, если любое случайное событие, связанное с одной из них не будет зависеть от любого события, определяемого другой случайной величиной.
Схемой Бернулли называются последовательные опыты, удовлетворяющие следующим условиям:
1. Число опытов фиксировано;
2. Каждый опыт приводит к одному из двух взаимно исключающих исходов, которые условно называются А - «успех»,  - «неудача»;
- «неудача»;
3. Вероятность «успеха» от опыта к опыту не меняются;
Опыты независимы.
39Центральная предельная теорема
Если случайные величины Х1, Х2,..., Хn,... попарно независимы, одинаково распределены и имеют конечную дисперсию, то при неограниченном увеличении n закон распределения случайной величины  неограниченно приближается к нормальному.
неограниченно приближается к нормальному.
40Геометрическое и биномиальное распределение
Закон распределения рассматриваемой дискретной случайной величины X, который может быть записан в виде бесконечного (но счетного) ряда распределения:
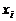
| 1 | 2 | 3 | 4 | ...... | i | ...... |

| 
| 
| 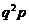
| 
| ...... | 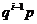
| ...... |
Очевидно, вероятности pi образуют геометрическую прогрессию со знаменателем q = 1 - р, поэтому такое распределение получило название геометрического.
Убедимся теперь в том, что сумма всех вероятностей 
 равна единице.
равна единице.

Теперь могут быть определены основные характеристики - математическое ожидание и дисперсия случайной величины X, распределенной по геометрическому закону. По определению математического ожидания:  .
.
В этой цепочке равенств штрих обозначает производную по переменной q.
Совершенно аналогично, правда несколько сложнее, может быть установлено, что дисперсия случайной величины X, распределенной по геометрическому закону, имеет следующий вид:  .
.
Формула Бернулли:

О случайной величине числа «успехов» в п испытаниях Бернулли - говорят, что она имеет биномиальное распределение с параметрами п и р.
Покажем, что сумма всевозможных вероятностей  , равна единице.
, равна единице.
Действительно:

Это соотношение представляет собой формулу бинома Ньютона. Поэтому и вероятностное распределение случайной величины числа «успехов» в п испытаниях Бернулли получило название биномиального распределения.
41Оценка вероятности по частоте. Характеристики этой оценки

Пусть производится серия из n одинаковых случайных опытов, относительной частотой (частостью) некоторого события А в этой серии называется отношение числа опытов nA, в которых это событие произошло, к общему числу произведенных опытов.
Статистической вероятностью Р(А) случайного события А называется относительная частота события А (при большом числе испытаний n): 
Несмотря на внешнее сходство полученного выражения с соотношением, используемым в классическом определении вероятности, эти формулы различны по существу.
Формула вычисления вероятности, основанная на классическом подходе, используется для теоретического использования. Для ее применения проведение опытов не требуется. Статистический подход по существу основывается на экспериментах, данные которых и позволяют определить вероятности случайных событий.
Теорема Бернулли. Пусть nA - частота появления события А в n независимых испытаниях и p есть вероятность наступления события А в каждом из испытаний. Тогда, для любого сколь угодно малого положительного числаε > 0,
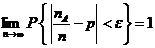 .
.
Другими словами это утверждение может быть сформулировано так: для любых сколь угодно малых положительных чисел ε и δ найдется такое натуральное число n0, что для любого n>n0 будет выполняться неравенство: 
Для проверки согласия теоремы Бернулли с опытом было проведено большое число экспериментов. При этом рассматривались события, вероятности которых можно считать по тем или иным соображениям известными, относительно которых легко проводить испытания и обеспечить независимость испытаний, а также постоянство вероятностей в каждом из испытаний. Все подобные опыты дали прекрасное совпадение с теорией.
42Независимые испытания, схема Бернулли
Пусть производится несколько испытаний. Если вероятность появления некоего события А в каждом из них не зависит от исходов остальных испытаний, то испытания независимы. При этом под словосочетанием «независимые испытания» часто подразумевают повторные независимые испытания – когда они осуществляются друг за другом.
Простейшие примеры:
– монета подбрасывается 10 раз;
– игральная кость подбрасывается 20 раз.
Схемой Бернулли называются последовательные опыты, удовлетворяющие следующим условиям:
1. Число опытов фиксировано;
2. Каждый опыт приводит к одному из двух взаимно исключающих исходов, которые условно называются А - «успех»,  - «неудача»;
- «неудача»;
3. Вероятность «успеха» от опыта к опыту не меняются;
Опыты независимы.
Очевидно, бросание n раз одной и той же монеты есть схема Бернулли с вероятностью успеха р, и вероятностью неудачи q =1-р. Если монета симметрична, то вероятность успеха р = 0,5 и вероятность неудачи q = 1 - р = 0,5.
43Доверительная вероятность и доверительный интервал
Доверительный интервал ‒ это промежуток числовой прямой, который с заранее заданной вероятностью, близкой к единице (доверительной вероятностью), накрывает оцениваемое значение искомого параметра.
44Интегральная предельная теорема Муавра-Лапласа
 2018-02-13
2018-02-13 298
298








