Локальная теорема Муавра-Лапласа. Свойства функции Гаусса

Локальная теорема Муавра – Лапласа. Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы 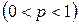, , величина ограничена равномерно по m и n, то вероятность появления события А ровно m раз в n независимых испытаниях приближенно равна

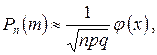
где - функция, значения которой определяются таблично.

График плотности нормального распределения называют нормальной кривой Гаусса.

Исследуем поведение функции плотности вероятности График плотности нормального распределения называют нормальной кривой Гаусса.

Исследуем поведение функции плотности вероятности f(x)

1. Очевидно, что функция определена на всей оси X

2. Функция принимает лишь положительные значения, т.е. нормальная кривая расположена над осью Ox.

3. Ось Ox служит горизонтальной асимптотой графика. Других асимптот у графика нет.

4. При x=a функция имеет максимум, равный Ø(x)max = 1/ σ корень 2п

5. Функция четная: ее график симметричен относительно прямой х=а

6. При х=а±σх график функции имеет точки перегиба.

При любых значениях параметров а и σ, площадь, ограниченная нормальной кривой и осью х равна единице.

Интегральная теорема Муавра-Лапласа. Свойства функции Лапласа.

Интегральная теорема Муавра-Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число m наступления события А в n независимых испытаниях заключено в пределах от а до b (включительно), при достаточно большом числе n приближенно равна Рn (a≤m≤b)= ½ [ Ф(х2) – Ф(х1)].