Пусть задана функция вещественного переменного  , определённая при
, определённая при  . Функция, которая подвергается преобразованию Лапласа, должна обладать следующими свойствами:
. Функция, которая подвергается преобразованию Лапласа, должна обладать следующими свойствами:
1. функция должна быть определена и дифференцируема по всей положительной полуоси;
2. функция должна быть тождественно равна 0 при  , т.е. (
, т.е. ( при
при  );
);
3. функция должна быть ограниченна, т.е. для функции  существуют такие положительные числа М и с, что
существуют такие положительные числа М и с, что  при
при  , т.е.
, т.е. 
 , где с – абсцисса абсолютной сходимости (некоторое положительное число).
, где с – абсцисса абсолютной сходимости (некоторое положительное число).
Т.о. для некоторой кусочно-непрерывной функции  , возрастающей при
, возрастающей при  не быстрее чем
не быстрее чем  , может быть поставлено в соответствие её преобразование Лапласа.
, может быть поставлено в соответствие её преобразование Лапласа.
Преобразованием Лапласа называют соотношение вида  ,
,
ставящее функции  вещественного переменного
вещественного переменного  в соответствие функцию
в соответствие функцию  комплексного переменного
комплексного переменного  (
( ).
).
При этом  называется оригиналом,
называется оригиналом,  – изображением, для обозначения соответствия между изображением и оригиналом используют знак соответствия «
– изображением, для обозначения соответствия между изображением и оригиналом используют знак соответствия « ».
».
Используется также символическая запись преобразования Лапласа, а именно,  , где
, где  – оператор прямого преобразования Лапласа,
– оператор прямого преобразования Лапласа,  - образ функции
- образ функции  является функцией комплексного переменного
является функцией комплексного переменного  , определяемой при
, определяемой при  .
.
Если функция тождественно равна 0 при  , то
, то  может быть однозначно определена (с точностью до значений в точках разрыва) по своему
может быть однозначно определена (с точностью до значений в точках разрыва) по своему  - образу, т.е.
- образу, т.е.  , где
, где  - оператор обратного преобразования Лапласа.
- оператор обратного преобразования Лапласа.
Рассмотрим несколько примеров:
1. 
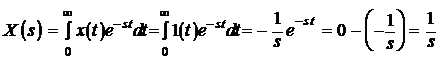 ;
; 
2. 

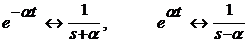
3. 


Преобразование Лапласа обладает следующими свойствами:
· Линейности:
если  , то
, то  , где
, где 
· Изменения масштаба во временной области:
если  то
то  .
.
· Смещения аргумента в области изображения (комплексной области):
пусть  , тогда
, тогда 
· Смещения аргумента в области оригинала (вещественной области):
пусть  , тогда
, тогда 
· Дифференцирования оригинала:
при ненулевых начальных условиях 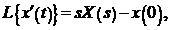
при нулевых начальных условиях  .
.

· Интегрирования оригинала при нулевых начальных условиях:
 .
.
· Свертки функций в действительной области:
 .
.
О предельных значениях:
 - теорема о начальном значении
- теорема о начальном значении
 - теорема о конечном значении.
- теорема о конечном значении.
 2018-02-13
2018-02-13 257
257







