2018-02-13
458
Вернёмся к записи дифференциального уравнения в виде
Пусть функции 
и 
являются непрерывными, дифференцируемыми, ограниченными и тождественно равными 0 при 
. Применим преобразование Лапласа при нулевых начальных условиях и получим
Обозначим: 
,
.
, где
- обычные функции комплексного переменного.
Изображение выходного сигнала системы имеет вид:
или 
.
Передаточной функцией в изображениях по Лапласу (ПФ) системы называется отношение изображения по Лапласу выходного сигнала 
к изображению по Лапласа входного сигнала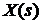 
при нулевых начальных условиях.
Комплексная передаточная функция преобразования «вход–выход» системы может быть получена заменой символа дифференцирования 
(или оператора дифференцирования) на комплексную переменную 
.
Передаточная функция представляет собой дробно-рациональную функцию, причем в реальной системе порядок числителя 
не превышает порядка знаменателя 
, т.е.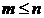 
. Коэффициенты передаточной функции 
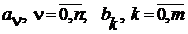вещественны, поскольку они представляют собой функции от вещественных параметров системы.
Значения 
, при которых ПФ обращается в нуль, называются нулями ПФ. Нули являются корнями уравнения
.
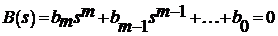Значения , при которых ПФ обращается в бесконечность, называются полюсами ПФ. Полюсы являются корнями уравнения
.
Передаточная функция 
имеет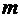 
нулей и 
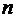полюсов. Нули и полюса могут быть действительными или комплексно-сопряженными, поэтому их можно изобразить на комплексной плоскости (s -плоскости).
Нули и полюса называются левыми (правыми), если они расположены в левой (правой) части s-плоскости, и нейтральными или нулевыми, если они лежат соответственно на мнимой оси или в начале координат.
