2018-02-13
1101
Колебательное звено. Имеем уравнение 
.
Примеры звеньев приведены на рис. 22.
Рис. 22. Примеры колебательных звеньев:
а - RLC -колебательный контур; б - механическая система (
- масса, 
- коэффициент упругости пружины, 
- коэффициент демпфирования)
Найдем ПФ. Имеем 
Тогда 
где 
или 
(при 
).
Параметры 
и называются коэффициентом усиления, постоянной времени и коэффициентом демпфирования(колебательности) колебательного звена соответственно.
При различных значениях имеют место следующие звенья:
· 
—консервативное или вырожденное колебательное (корни чисто мнимые);
· 
— апериодическое 2-го порядка (корни вещественные);
· 
— колебательное корни комплексно-сопряжённые).
Рассмотрим колебательное звено.
Найдём корни характеристического уравнения 
.
, где
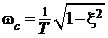- частота собственных колебаний звена,
- сопрягающая частота системы.
Вещественная часть корня представляет собой коэффициент затухания переходного процесса; мнимая часть корня – частоту колебаний переходного процесса.
Для получения временных характеристик можно воспользоваться таблицей оригиналов и изображений или соответствующей аналитической формулой.
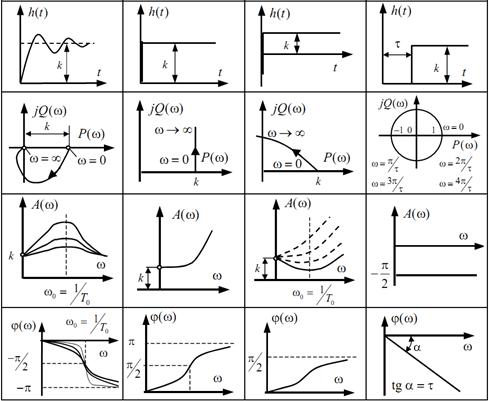
Запишем выражение для ИПФ колебательного звена (рис. 23).
.
Перед построением ИПФ определим начальные и конечные значения:
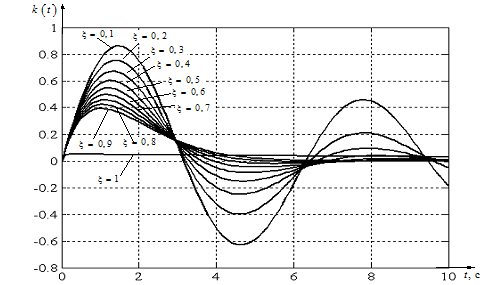
Рис. 23.ИПФ колебательного звена (
)
Определим переходную функцию колебательного звена (рис. 24).
Перед построением переходной функции определим начальные и конечные значения:
Рис. 24.Переходная характеристика колебательного звена
при различных значениях 
Перейдем к рассмотрению частотных характеристик.
АФЧХ колебательного звена представлены на рис. 25.
Рис. 25.АФЧХ колебательного звена.
Определим значение АЧХ в контрольных точках: 
Амплитудная характеристика плавно уменьшается, если 
. Если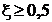 
, то на амплитудной характеристике появляется резонансный «горб».
Частота, при которой амплитудная характеристика достигает максимального значения, называется резонансной и определяется формулой
.
Частота 
как в случае апериодического звена, так и в случае колебательного звена называется сопрягающей частотой.
ФЧХ имеет вид 
Определим значение ФЧХ в контрольных точках:
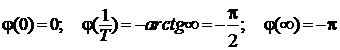
Графики 
и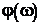 
изображены на рис. 26.
Рис. 26.АЧХ и ФЧХ колебательного звена для различных значений .
Построим асимптотическую ЛАЧХ: 
1. Пусть 
, тогда в выражении 
пренебрегают вторым слагаемым и 
и характеристика в этой области представляет собой прямую, параллельную оси абсцисс.
2. Если 
, то в выражении во втором слагаемом оставляют только наибольшее слагаемое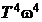 
, тогда 
.
Характеристика в этой области представляет собой прямую с наклоном -40 дб/дек.
Определим значение функции на частоте сопряжения
На рис. 27 и 28 показаны асимптотическая ЛАЧХ и ЛФЧХ колебательного звена для различных значений .
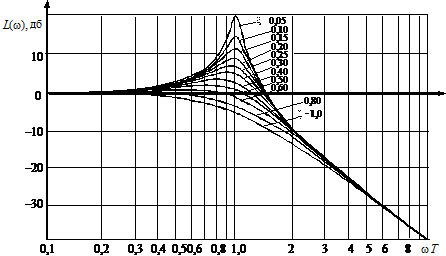
Рис. 27.ЛАЧХ колебательного звена при различных значениях
Рис. 28.ЛФЧХ колебательного звена при различных значениях 
Рассматривая колебательное звено в общем виде, мы получаем в качестве частных случаев ещё 2 типовых звена: консервативное и апериодическое второго порядка.
.
Есть звенья, которые традиционно относятся к типовым и указываются в таблицах, но при этом они не являются простейшими. К ним относятся:
-интегрирующеес замедлением или инерционное интегрирующее;
-дифференцирующее с замедлением (инерционное дифференцирующее);
-интегро- дифференцирующее, если 
, то звено ближе к интегрирующему; если 
, то звено ближе к дифференцирующему.
Неминимально – фазовые звенья.
Важным общим показателем типовых звеньев является принадлежность нулей передаточной функции к левой полуплоскости комплексного переменного.
Пусть имеем: 
, где
- полюса знаменателя; 
-нули числителя. Рассмотрим один из сомножителей знаменателя 
. Звенья, нули и полюса которых лежат в левой полуплоскости, называют минимально-фазовыми. Звенья, передаточные функции которых имеют нули и полюса, лежащие в правой полуплоскости, называются неминимально-фазовыми.
