2018-02-13
592
Потоки платежей – платежи, последовательные во времени (например, з/п).
Регулярным потоком платежей (финансовой рентой, аннуитетом) называются платежи, у которых все выплаты направлены в одну сторону, например, поступления, а интервал между платежами одинаковый.
Свойства:
- Выплаты направлены в одну стороны
- Интервал между платежами одинаковый
Нерегулярный поток платежей - тот, в котором хотя бы одно из 2х свойств не удовлетворяется.
Наращенная сумма потока платежей – сумма всех выплат с начисленными на них к концу срока сложными процентами.
Современная стоимость потоков платежей - сумма всех выплат, дисконтированных на начало срока этого потока по сложной процентной ставке.
* Дисконтирование – процесс определения современной стоимости будущего платежа.
По моменту выплат в пределах между началом и концом периода ренты делятся на:
- Ренты-постнумеранто – выплаты производятся в конце периода (чаще всего)
- Ренты-пренумеранто – выплаты производятся в начале периода
- Ренты с платежами в середине периода
|
|
|
Годовая рента-постнумеранто.
Предусматривает выплаты и начисления процентов один раз в конце года.
R – величина годовой выплаты.
n – срок ренты.
S =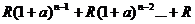 
Представляет собой сумму геометрической прогрессии со знаменателем (1+а).
S = R*sn;a (наращенная сумма)
sn;a - коэффициент наращения ренты (табулированная функция).
А = R*an;a ( современная стоимость ренты )
an;a = 
( коэффициент приведения)
Пример 1.
В фонд ежегодно в конце года поступают средства по 10 000 руб. в течение 7 лет, на которые начисляются проценты – 15% годовых. Определить коэффициенты наращения-приведения ренты, а также величину фонда на конец срока и его современную стоимость.
Более общим типом является рента с начислением процентов по номинальной процентной ставке и с неоднократными выплатами в году.
m – количество начислений процентов в году
p – количество выплат в году
Если выплаты производятся р раз в году, то такая рента называется р-срочная. В любом году производится р выплат по R/p руб., где R – годовая выплата. Срок ренты – n лет. В этом случае наращенная сумма S и современная стоимость А:
S = R*s(p)mn; j/m
A = R*a(p)mn; j/m
s(p)mn; j/m = 
a(p)mn; j/m = 
Пример 2.
В фонд ежегодно в конце года поступают средства по 10 000 руб. в течение 7 лет, на которые начисляются проценты по номинальной процентной ставке – 15% годовых, начисляется поквартально (n=4). Определить коэффициенты наращения-приведения ренты, а также величину фонда на конец срока и его современную стоимость.
Пример 3.
Кредит = 1000 руб., выдается на 4 года. Выплаты производятся ежемесячно (в конце месяца). n = 1. Ставка по кредиту = 20%. Найти разовую выплату.
|
|
|
