Определение 1. Функциональный ряд 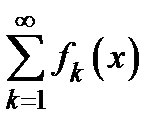 сходится в точке
сходится в точке  , если числовой ряд
, если числовой ряд  является сходящимся. Совокупность
является сходящимся. Совокупность  таких точек (точек сходимости) называется множеством сходимости (или областью сходимости) ряда. Говорят ещё, что ряд поточечно сходится на множестве
таких точек (точек сходимости) называется множеством сходимости (или областью сходимости) ряда. Говорят ещё, что ряд поточечно сходится на множестве  . (Отметим, что
. (Отметим, что  может быть совершено произвольным подмножеством числовой прямой.)
может быть совершено произвольным подмножеством числовой прямой.)
Пусть  − полная сума, n -я частичная сумма и n -й остаток ряда.
− полная сума, n -я частичная сумма и n -й остаток ряда.  . Поточечная сходимость ряда на множестве
. Поточечная сходимость ряда на множестве  означает, что
означает, что 
 в каждой точке
в каждой точке  .
.
Определение 2. Ряд  равномерно сходится на множестве
равномерно сходится на множестве  , если
, если 
 . Это означает другими словами, что последовательность частичных сумм
. Это означает другими словами, что последовательность частичных сумм  равномерно сходится
равномерно сходится  к сумме ряда
к сумме ряда  или
или  Ã
à  (т.к.
(т.к.  ).
).
Ясно, что из равномерной сходимости  следует поточечная сходимость на этом множестве, Обратная импликация не верна.
следует поточечная сходимость на этом множестве, Обратная импликация не верна.
Контрпример.Рассмотрим на отрезке  последовательность функций последовательность функций  или ряд или ряд .В этом примере .В этом примере  . Однако . Однако 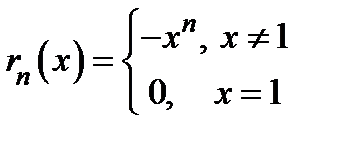 , следовательно, , следовательно,  . . |  |
Критерий Коши равномерной сходимости ряда. Ряд  равномерно сходится на множестве
равномерно сходится на множестве  тогда и только тогда, когда
тогда и только тогда, когда 
 .
.
Доказательство. Необходимость условия Коши сразу следует из равенства  .
.
Предположим теперь, что условие Коши выполнено. Тогда последовательность  поточечно фундаментальна и, следовательно, имеет
поточечно фундаментальна и, следовательно, имеет  поточечный предел, скажем
поточечный предел, скажем  . Кроме того, в силу условия Коши
. Кроме того, в силу условия Коши  , существует
, существует  номер
номер  такой, что
такой, что 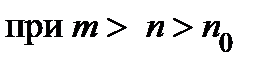
будет  всюду на множестве
всюду на множестве  . Переходя к поточечному пределу
. Переходя к поточечному пределу  , видим, что
, видим, что  всюду
всюду  или
или  .
.
Таким образом,  Ã
à 
 .
.
Следствие (Признак Вейерштрасса равномерной сходимости ряда). Если функциональный ряд  мажорируется на множестве
мажорируется на множестве  сходящимся числовым рядом
сходящимся числовым рядом  (т.е.
(т.е.  ), то данный функциональный ряд равномерно сходится
), то данный функциональный ряд равномерно сходится  .
.
Доказательство. Если  и при всех значениях
и при всех значениях  , а ряд
, а ряд  сходится, то
сходится, то  . Поэтому
. Поэтому 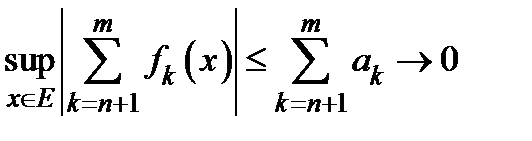
 .
.
В таком случае согласно критерию Коши ряд  равномерно сходится на множестве
равномерно сходится на множестве  .
.
Признак Абеля равномерной сходимости ряда. Рассмотрим ряд вида  .
.
Предположим, что выполнены следующие условия:
1) ряд  равномерно сходится на множестве
равномерно сходится на множестве  ,
,
2) последовательность  равномерно ограничена
равномерно ограничена 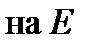 , т.е. существует такое положительное число
, т.е. существует такое положительное число  , что
, что  ,
,
3) при любом фиксированном значении 
 − монотонная последовательность.
− монотонная последовательность.
В таком случае ряд равномерно сходится на множестве  .
.
*Доказательство. Обозначим 
 остаток ряда
остаток ряда  и
и  . Из условия 1) следует, что
. Из условия 1) следует, что  , когда
, когда 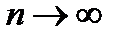 . Оценим величину
. Оценим величину  .
.


 .
.
Поэтому 
 ввиду монотонности последовательности
ввиду монотонности последовательности  . Следовательно,
. Следовательно, 
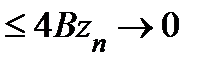 . Остаётся воспользоваться критерием Коши равномерной сходимости ряда.
. Остаётся воспользоваться критерием Коши равномерной сходимости ряда.
 2018-02-13
2018-02-13 5325
5325








