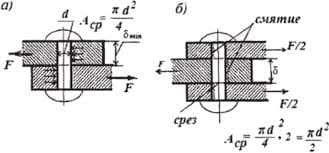
Теорема о единственности степенного разложения. Если 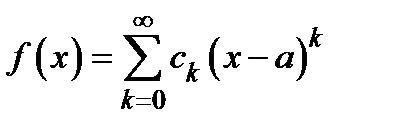
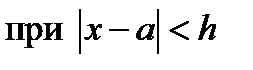 , то
, то 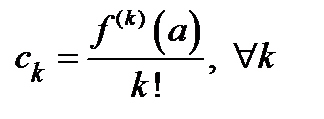 и, следовательно,
и, следовательно, 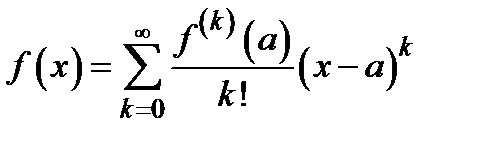 (ряд Тейлора).
(ряд Тейлора).
Доказательство. Повторно дифференцируя исходное тождество, получаем
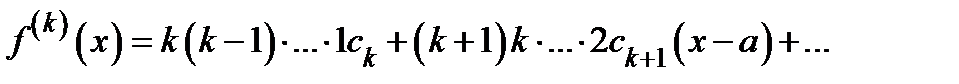 .. Поэтому
.. Поэтому 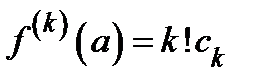 . Ч и т.д.
. Ч и т.д.
Как мы уже знаем, для представимости функции в виде суммы степенного ряда на интервале необходимо, чтобы эта функция была там бесконечно дифференцируемой. Это условие, однако, не является достаточным.
Контрпример. Пусть 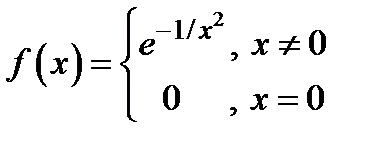 . Нетрудно доказать, что
. Нетрудно доказать, что 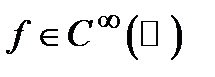 , в частности,
, в частности, 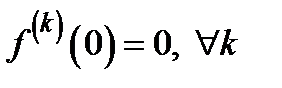 . В то же время,
. В то же время,  невозможно представить в виде
невозможно представить в виде 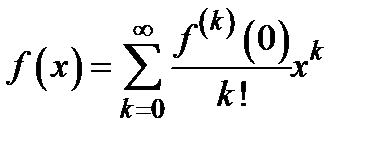 , иначе было бы
, иначе было бы 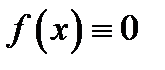 , что неверно, так как
, что неверно, так как 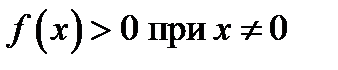 .
.
Сформулируем теперь достаточное условие представимости функции рядом Тейлора. Введём для этого величины 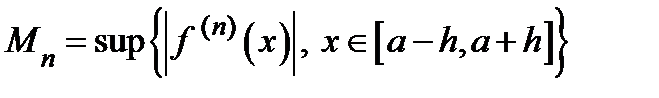 .
.
Теорема. Если последовательность чисел 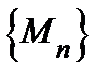 ограничена, то
ограничена, то 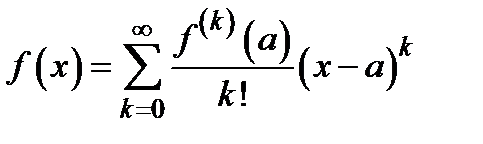
на отрезке 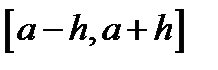 .
.
Пользуясь этой теоремой и конечной формулой Тейлора для функций 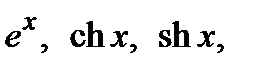
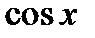 и
и 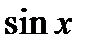 , получаем разложения в ряд Тейлора этих функций на всей числовой оси:
, получаем разложения в ряд Тейлора этих функций на всей числовой оси:
1) 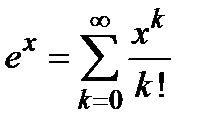 ; 2)
; 2) 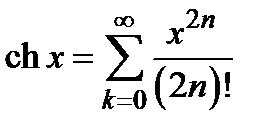 ; 3)
; 3) 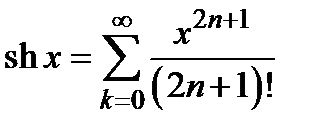 ;
;
4)  ; 5)
; 5) 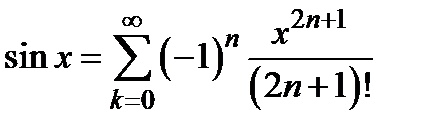 .
.
Немного сложнее обосновать разложения:
6) 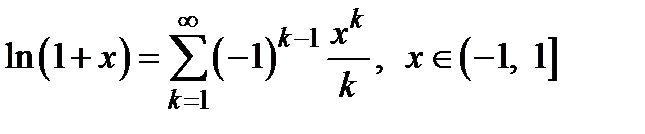 ; 7)
; 7) 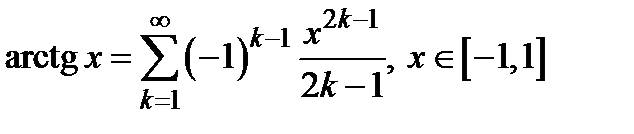 ;
;
8) 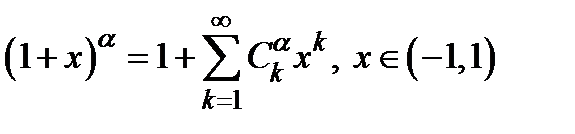 .
.
В последнем разложении используется обозначение 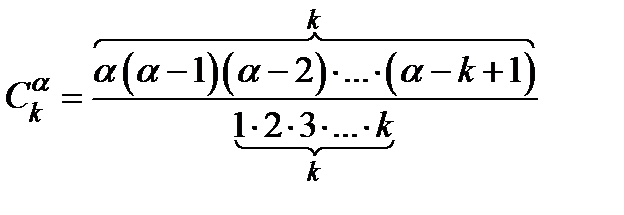 .
.
Некоторые приложения степенных рядов.
Пример 1. Вычислить суммы рядов 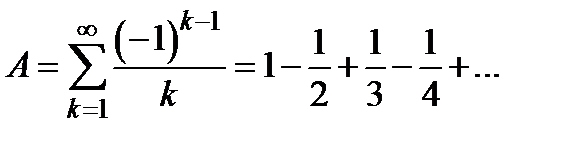 (ряд Лейбница) и
(ряд Лейбница) и 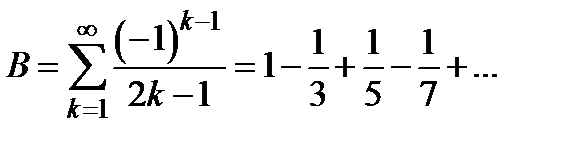 .
.
Решение. Если подставить 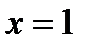 в обе части разложений 6) и 7), то сразу же получим
в обе части разложений 6) и 7), то сразу же получим
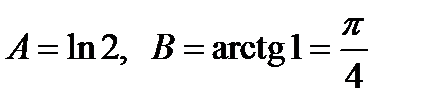 .
.
Дополнение. Ряды из примера 1 непригодны для вычислений, они слишком медленно сходятся. Так, остаток  ряда
ряда 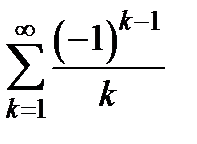 убывает со скоростью
убывает со скоростью 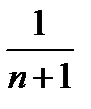 и для вычисления с точностью
и для вычисления с точностью 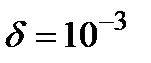 необходимо просуммировать 1000 членов ряда. Покажем на том же примере, что метод степенных рядов может давать отличные результаты, если алгоритм вычислений немного усовершенствовать. Снова обратимся к табличному разложению 6). Это даёт нам
необходимо просуммировать 1000 членов ряда. Покажем на том же примере, что метод степенных рядов может давать отличные результаты, если алгоритм вычислений немного усовершенствовать. Снова обратимся к табличному разложению 6). Это даёт нам  :
:
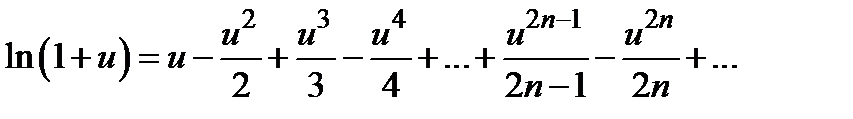 ,
,
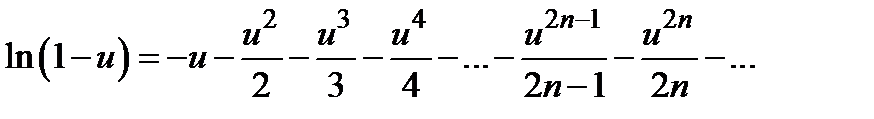 .
.
Следовательно, 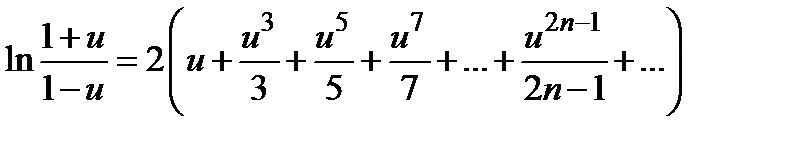 . Замена
. Замена 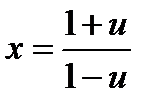 приводит к тождеству
приводит к тождеству 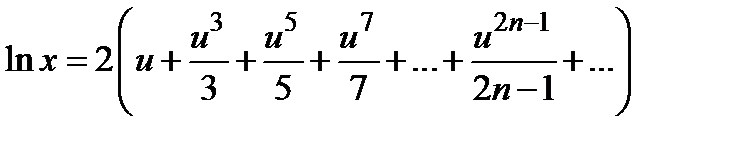 . Здесь
. Здесь 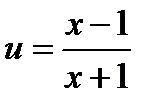 и если
и если 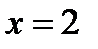 , то
, то 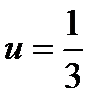 .
.
Поэтому 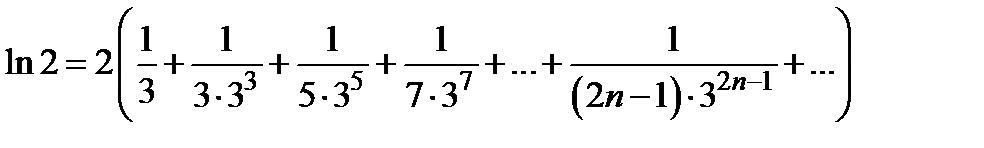 . Этот ряд сходится гораздо быстрее.
. Этот ряд сходится гораздо быстрее.
Сейчас 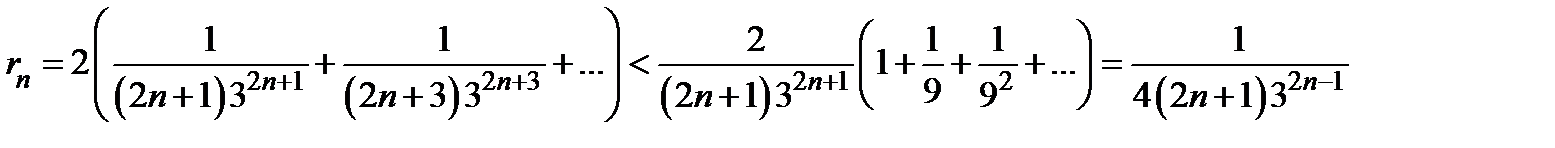 .
.
В частности, 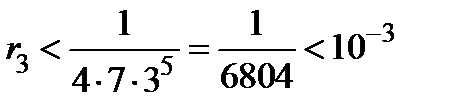 , а потому с точностью
, а потому с точностью  будет
будет 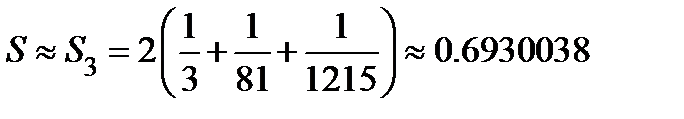 . Отбрасывая ненадёжные знаки, получаем
. Отбрасывая ненадёжные знаки, получаем 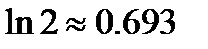 . Для уменьшения погрешности вычислений нужно увеличить количество учитываемых членов ряда. Так, например,
. Для уменьшения погрешности вычислений нужно увеличить количество учитываемых членов ряда. Так, например, 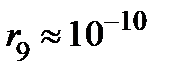 , поэтому
, поэтому 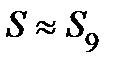 с точностью
с точностью 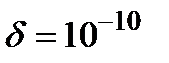 .
.
Пример 2. Вычислить с точностью 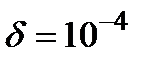 интеграл
интеграл 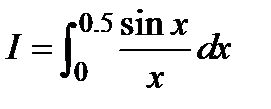 .
.
Решение. Так как 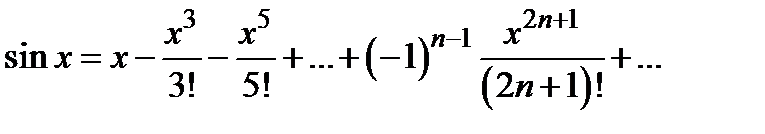 , то
, то 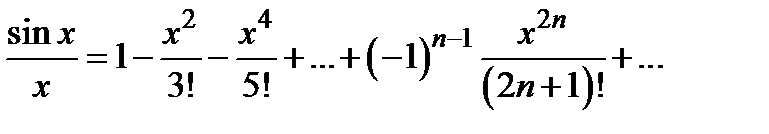 .
.
Поэтому 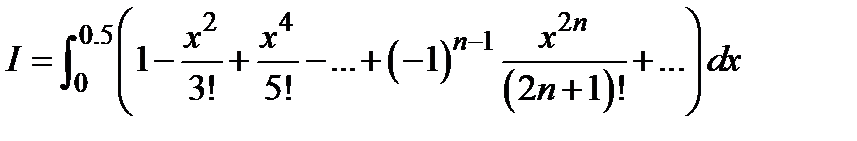 =
= 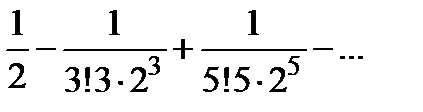 .
.
По теореме Лейбница 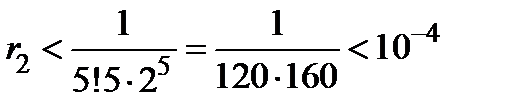 , то
, то 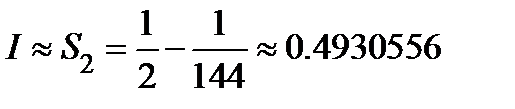 . Округляя, получаем с нужной точностью
. Округляя, получаем с нужной точностью 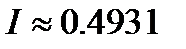 .
.
Пример 3. Найти приближенное решение уравнения 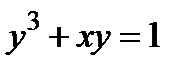 вблизи
вблизи 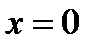 .
.
Решение. Ясно, что 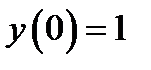
 2018-02-13
2018-02-13 454
454