Определение. Степенным рядом называется функциональный ряд вида
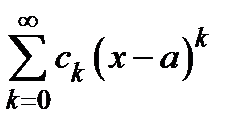 . (1)
. (1)
Числа  называются коэффициентами ряда (1), число
называются коэффициентами ряда (1), число 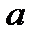 − центром сходимости.
− центром сходимости.
Первая теорема Абеля о степенных рядах. Если ряд (1) сходится  , то он сходится при всех значениях
, то он сходится при всех значениях  , более близких к центру сходимости
, более близких к центру сходимости 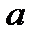 (т.е. сходится
(т.е. сходится  ).
).
Доказательство. По условию ряд  сходится. Согласно необходимому условию сходимости ряда, последовательность его членов стремится к нулю а, значит ограничена. Это означает, что существует
сходится. Согласно необходимому условию сходимости ряда, последовательность его членов стремится к нулю а, значит ограничена. Это означает, что существует 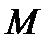 большее, чем все величины
большее, чем все величины  , т.е.
, т.е. 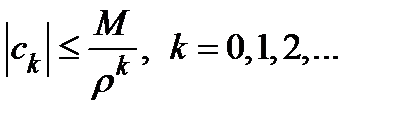 .
.
Выберем произвольное положительное число  . Для любого
. Для любого  , для которого
, для которого  , справедливо неравенство
, справедливо неравенство 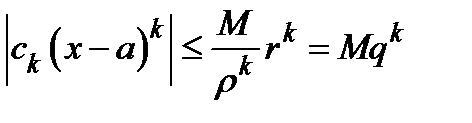 , где
, где  . Признак сравнения показывает, что при любом таком значении
. Признак сравнения показывает, что при любом таком значении 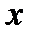 ряд (1) сходится.
ряд (1) сходится.
Замечание. Мы доказали несколько больше: на отрезке  ряд (1) мажорируется рядом
ряд (1) мажорируется рядом 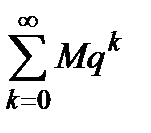
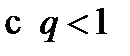 .
.
Следствие. Существует  такое, что ряд (1) сходится
такое, что ряд (1) сходится 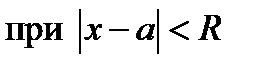 и расходится
и расходится 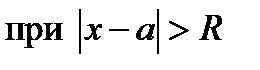 . (Такое
. (Такое  называется радиусом сходимости степенного ряда (1), а промежуток
называется радиусом сходимости степенного ряда (1), а промежуток  − интервалом сходимости.)
− интервалом сходимости.)
Доказательство. Теорема Абеля показывает, что таким числом является 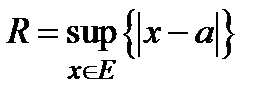 , где
, где  − область сходимости ряда (1), т.е. множество значений
− область сходимости ряда (1), т.е. множество значений  , при которых ряд сходится.
, при которых ряд сходится.
Теорема. Если существует предел  , то справедлива формула
, то справедлива формула  (здесь подразумевается, что
(здесь подразумевается, что  и
и 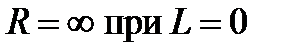 ).
).
Доказательство. Внутри интервала сходимости степенной ряд абсолютно сходится, поэтому нам придётся исследовать ряд (1) на абсолютную сходимость. Применяем признак Даламбера. Так как 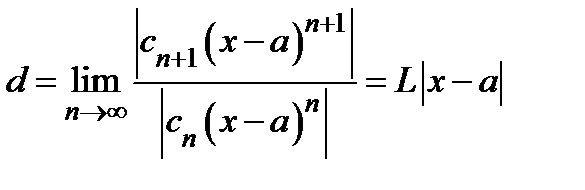 , то ряд
, то ряд 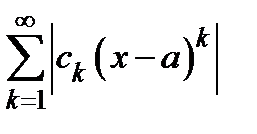 сходится, когда
сходится, когда 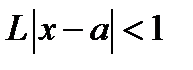 , и расходится, когда
, и расходится, когда  . Поэтому
. Поэтому 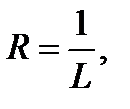 если
если 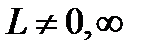 .
.
Доказательство упрощается в случае, когда 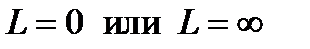 (в первом случае
(в первом случае 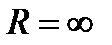 , во втором ―
, во втором ―  .)
.)
Замечание. В доказанной формуле предел 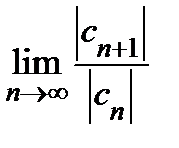 можно заменить
можно заменить  . Самый общий случай описывается формулой
. Самый общий случай описывается формулой 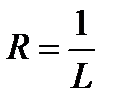 , где
, где  (формула Коши – Адамара).
(формула Коши – Адамара).
Пример. Найти область сходимости рядов 1)  , 2)
, 2) 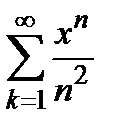 , 3)
, 3)  4)
4) 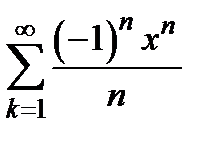 .
.
Решение. Во всех четырёх случаях интервал сходимости это −  , так как
, так как 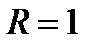 . В первом из примеров ряд расходится в обеих концевых точках этого интервала. Во втором − сходится в точках
. В первом из примеров ряд расходится в обеих концевых точках этого интервала. Во втором − сходится в точках  . В третьем примере ряд сходится только в левом конце, а в четвертом примере − только в правом.
. В третьем примере ряд сходится только в левом конце, а в четвертом примере − только в правом.
Следствие формулы Коши - Адамара. При формальном дифференцировании и интегрировании степенного ряда его радиус сходимости не изменяется.
Доказательство. После формального дифференцирования и интегрирования ряда 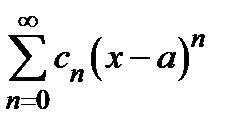 получим два новых степенных ряда
получим два новых степенных ряда  . Если существует предел
. Если существует предел
 , то , то  . Поэтому . Поэтому
|  . .
|
Это равенство легко обобщается на общий случай.
Теорема. Внутри интервала сходимости степенной ряд допускает почленное интегрирование и почленное дифференцирование. В частности, у суммы ряда есть производная и она равна сумме производных от членов ряда.
Доказательство. Это утверждение является следствием того факта, что по теореме Абеля степенной ряд равномерно сходится на любом отрезке, лежащем внутри его интервала сходимости, и теорем о почленном интегрировании и дифференцировании общих функциональных рядов.
Следствие. Внутри интервала сходимости сумма степенного ряда является бесконечно дифференцируемой функцией.
Вторая теорема Абеля о степенных рядах. Если степенной ряд 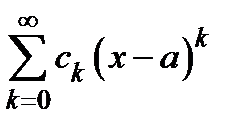 сходится в конце интервала сходимости, то его сумма
сходится в конце интервала сходимости, то его сумма 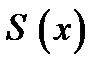 односторонне непрерывна в этой конечной точке.
односторонне непрерывна в этой конечной точке.
*Доказательство. Пусть, например, ряд сходится в точке  , где
, где 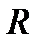 − радиус сходимости степенного ряда и пусть
− радиус сходимости степенного ряда и пусть 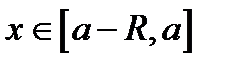 . Тогда
. Тогда 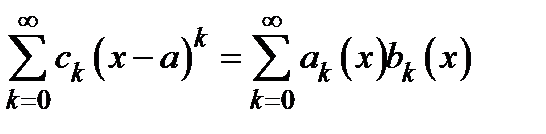 ,
,
где  ,
,  . По условию теоремы ряд
. По условию теоремы ряд 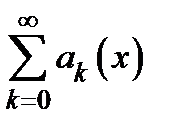 сходится, а так как это − ряд с постоянными членами, то он равномерно сходится. Что же касается
сходится, а так как это − ряд с постоянными членами, то он равномерно сходится. Что же касается  , то при любом
, то при любом 
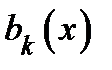 − монотонная последовательность и
− монотонная последовательность и  .
.
По теореме Абеля из §4 рассматриваемый ряд равномерно сходится на отрезке  . Теорема о непрерывности суммы ряда из §5 показывает, что функция
. Теорема о непрерывности суммы ряда из §5 показывает, что функция  непрерывна
непрерывна  , в частности, эта функция непрерывна справа в точке
, в частности, эта функция непрерывна справа в точке  .
.
 2018-02-13
2018-02-13 544
544








