Предположим, что поверхность 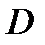 задана явным уравнением
задана явным уравнением  , где
, где 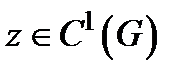 .
.
Угол  между касательной плоскостью к поверхности
между касательной плоскостью к поверхности 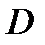 и плоскость XOY равен углу между нормальным вектором
и плоскость XOY равен углу между нормальным вектором  и ортом
и ортом 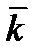 . Поэтому
. Поэтому 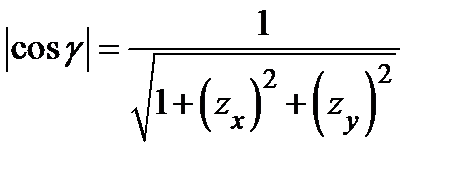 , а связь между площадью элемента касательной плоскости
, а связь между площадью элемента касательной плоскости 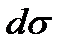 и
и
площадью его проекции 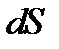 на плоскость XOY выглядит следующим образом:
на плоскость XOY выглядит следующим образом:
 | 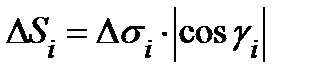 или или 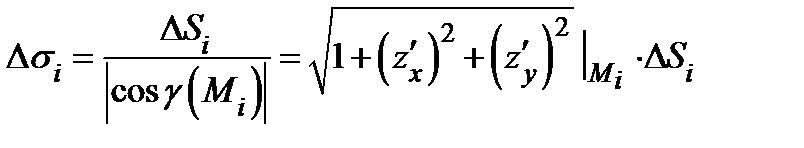 . Рассмотрим теперь площадь “описанного многогранника” . Рассмотрим теперь площадь “описанного многогранника”  . . |
Определение. Если существует предел 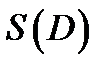 суммы
суммы  при условии, что мелкость разбиения
при условии, что мелкость разбиения 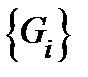 стремится к нулю, будем считать этот предел площадью поверхности
стремится к нулю, будем считать этот предел площадью поверхности 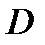 . Ясно, что
. Ясно, что 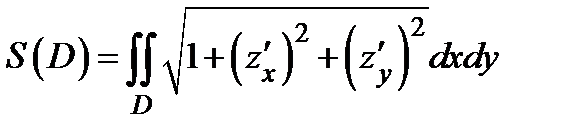 .
.
Пример. Найти площадь 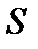 части параболоида вращения
части параболоида вращения 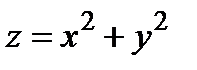 , отсекаемой плоскостью
, отсекаемой плоскостью  .
.
Решение. 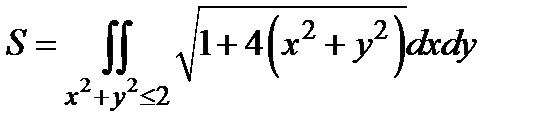
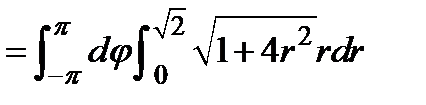 =
= 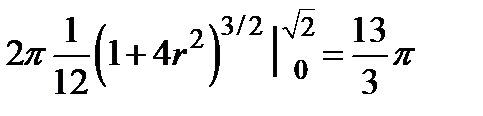 .
.
2˚. Физические приложения кратных интегралов.
Массу тела  можно найти по формуле
можно найти по формуле 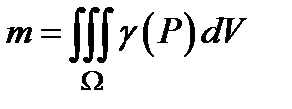 , где
, где 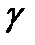 объёмная плотность материала, массу пластины − по формуле
объёмная плотность материала, массу пластины − по формуле 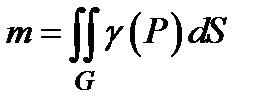 (на этот раз
(на этот раз 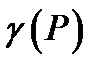 − поверхностная плотность). Точно так же, заряд
− поверхностная плотность). Точно так же, заряд 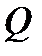 можно вычислить, интегрируя объёмную (поверхностную) плотность распределения заряда.
можно вычислить, интегрируя объёмную (поверхностную) плотность распределения заряда.
Центр масс:  , здесь
, здесь 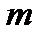 − снова масса тела
− снова масса тела  .
.
Напряженность в точке 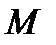 гравитационного поля, создаваемого массой, распределённой с плотностью
гравитационного поля, создаваемого массой, распределённой с плотностью 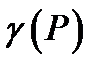 , равна
, равна  , где
, где 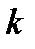 − гравитационная постоянная. Потенциал гравитационного поля равен
− гравитационная постоянная. Потенциал гравитационного поля равен 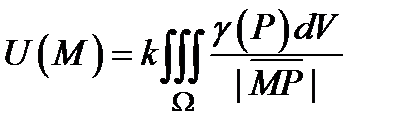 .
.
Моменты инерции:  ,
, 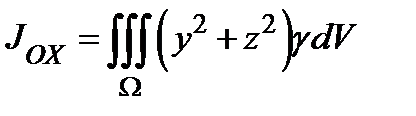 ,
,  и т.д.
и т.д.
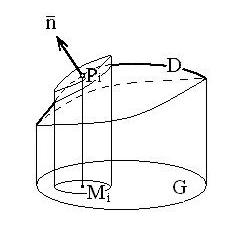
Пример. Доказать, что однородный шар притягивает материальную точку, находящуюся вне шара, так, как если бы вся масса шара была сосредоточена в его центре.
Решение. Если расположитьшар и точку  так, как показано на рисунке, будет
так, как показано на рисунке, будет  . Вычислим
. Вычислим 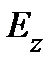 , считая, что
, считая, что 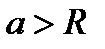 .
.
 | 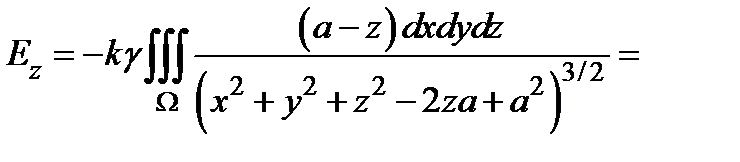 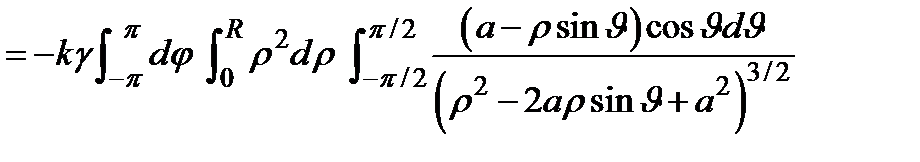 . Сделаем во внутреннем интеграле следующую замену: . Сделаем во внутреннем интеграле следующую замену: 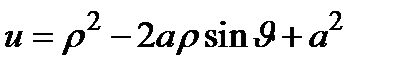 . При этом будет . При этом будет  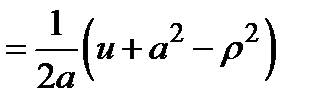 , , 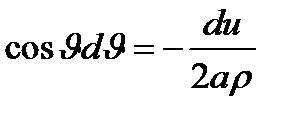 ; ; 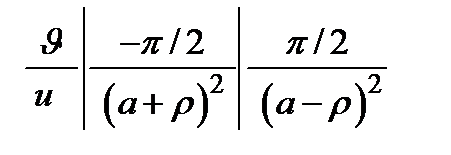 . . 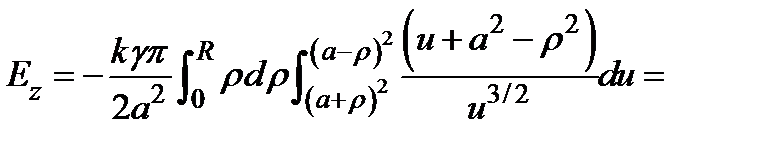 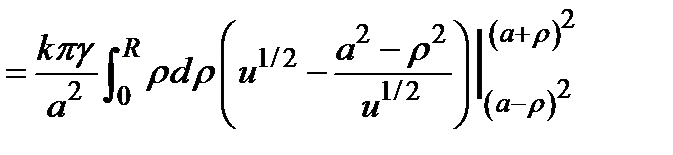 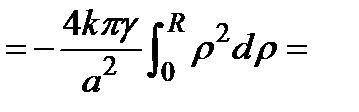  , где , где 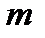 − масса шара. − масса шара. |
Понятие о несобственных кратных интегралах*.
Мы не станем здесь углубляться в теорию, а рассмотрим лишь один пример: 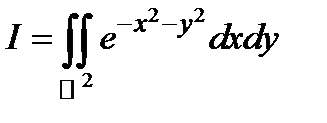 .
.
Мы можем определить его как предел частичного интеграла разными способами. Например,
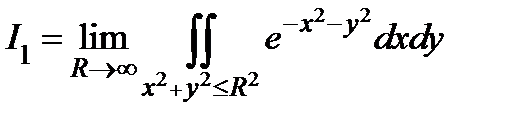 или
или 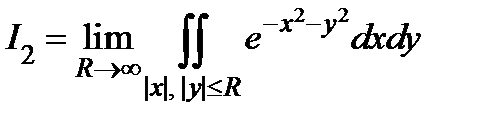 .
.
1.  =
= 
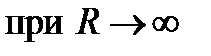 .Следовательно,
.Следовательно, 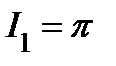 .
.
2. Так как подынтегральная функция положительна, то интеграл возрастает с расширением области.
Поэтому 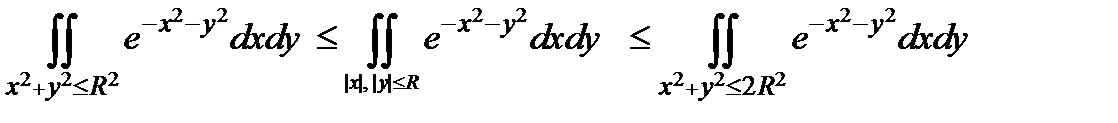 . Следовательно,
. Следовательно, 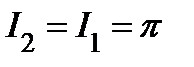 . Воспользуемся этим, результатом для вычисления интеграла Пуассона
. Воспользуемся этим, результатом для вычисления интеграла Пуассона  .
.
Имеем 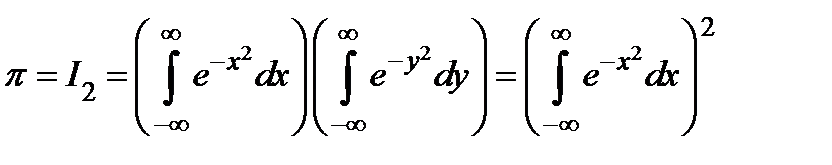 . Поэтому
. Поэтому 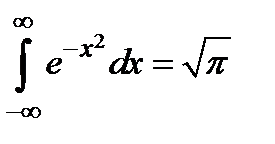 .
.
Отметим, что для теории вероятностей и других дисциплин важным является следствие этой формулы 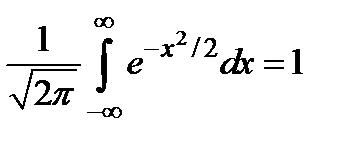 .
.
Формула Грина (связь криволинейного интеграла на плоскости с двойным).
1˚. Криволинейный интеграл по координатам.
Пусть 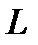 − кривая, заданная параметрическими уравнениями
− кривая, заданная параметрическими уравнениями 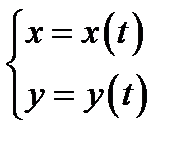 ,
, 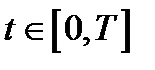 ; и пусть
; и пусть 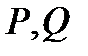 − функции, определенные в точках этой кривой. Рассмотрим разбиение отрезка
− функции, определенные в точках этой кривой. Рассмотрим разбиение отрезка 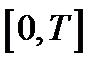 точками
точками 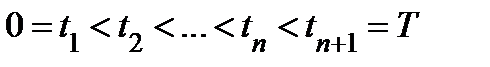 , выберем промежуточные значения
, выберем промежуточные значения 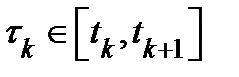 и обозначим
и обозначим  току кривой
току кривой  с координатами
с координатами  . Составим интегральную сумму
. Составим интегральную сумму 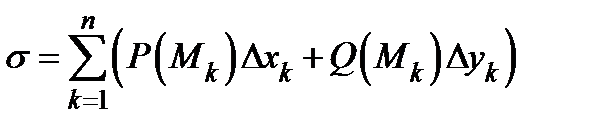 (здесь
(здесь 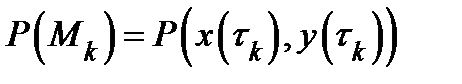 , а
, а 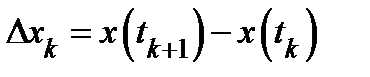 и т.д.).
и т.д.).

Определение. Если существует предел 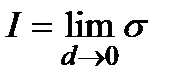 , где
, где 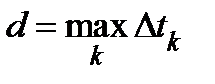 , то он называется криволинейным интегралом по координатам и обозначается
, то он называется криволинейным интегралом по координатам и обозначается 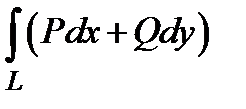 .
.
Для вычисления криволинейного интеграла следует превратить его в определённый интеграл с помощью “замены переменной”. Точнее, справедлива
Теорема. Если  − гладкая кривая, а функции
− гладкая кривая, а функции  непрерывны вдоль этой кривой, то существует криволинейный интеграл,
непрерывны вдоль этой кривой, то существует криволинейный интеграл,  при этом
при этом  , где
, где 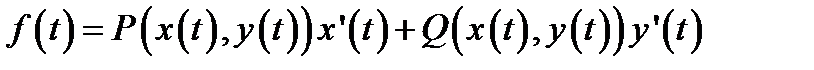 .
.
Помимо обычных свойств интеграла, вроде аддитивности по дуге и линейности, справедливо ещё одно: интеграл вдоль границы области, является аддитивной функции самой области.
Поясним формулировку нового свойства рисунком. В изображенной на рисунке конфигурации интегралы по дугам AB и BA взаимно уничтожатся.
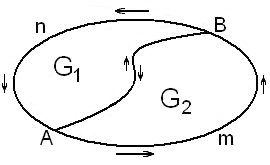
Формула Грина.
Теорема. Пусть 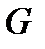 − область на плоскости
− область на плоскости  , граница которой
, граница которой 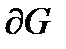 − замкнутая кусочно-гладкая кривая, и пусть функции
− замкнутая кусочно-гладкая кривая, и пусть функции 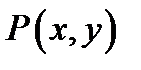 и
и 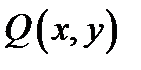 непрерывно дифференцируемы в замкнутой области
непрерывно дифференцируемы в замкнутой области  . В таком случае справедливо равенство:
. В таком случае справедливо равенство:
 . (1)
. (1)
Здесь 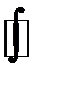 означает интегрирование вдоль замкнутой кривой, которая обходится против направления движения часовой стрелки.
означает интегрирование вдоль замкнутой кривой, которая обходится против направления движения часовой стрелки.
Доказательство.
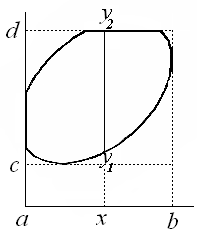
1. Выведем сначала формулу (1) в том случае, когда область 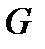 является простой
является простой
(т.е. сечения области координатными прямыми содержат не более одного отрезка).
а) Так как 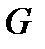 простая, то.
простая, то. 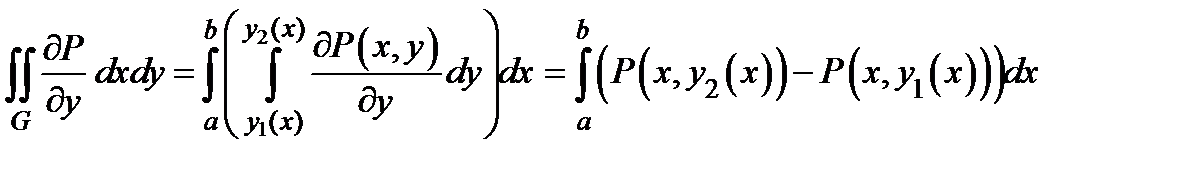
С другой стороны,  . Следовательно,
. Следовательно, 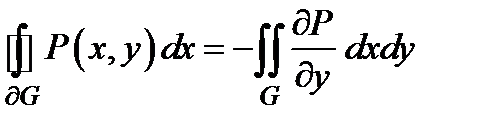 .
.
б) Точно так же доказывается, что 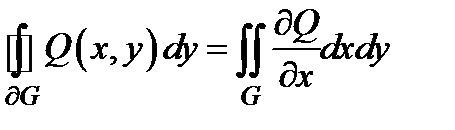 . Складывая два полученных равенства, приходим к формуле (1).
. Складывая два полученных равенства, приходим к формуле (1).
2. Покажем на примере кругового кольца  , что формула Грина верна и для областей, которые можно разбить на несколько простых областей.
, что формула Грина верна и для областей, которые можно разбить на несколько простых областей.
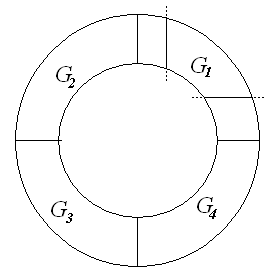 | Каждая из частей 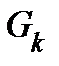 , на которые разрезано кольцо, является простой, поэтому , на которые разрезано кольцо, является простой, поэтому 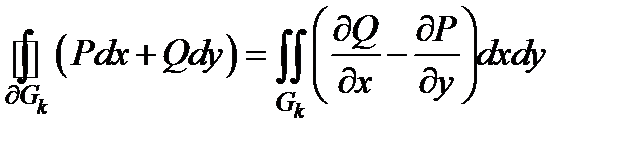 , ,  . Сложим эти четыре равенства. Сумма левых частей равна . Сложим эти четыре равенства. Сумма левых частей равна 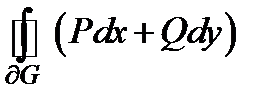 . Сумма правых частей равна . Сумма правых частей равна 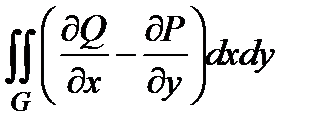 . Это показывает, что формула Грина верна для кольца . Это показывает, что формула Грина верна для кольца  . . |
Глава 8. Ряды.
 2018-02-13
2018-02-13 796
796