Теорема 1. (О непрерывности предела последовательности). Если последовательность непрерывных на отрезке  функций
функций  равномерно сходится
равномерно сходится 
 , то
, то  непрерывна на этом отрезке.
непрерывна на этом отрезке.
Доказательство. Для любого  найдётся номер
найдётся номер 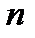 такой, что
такой, что  .
.
По теореме Кантора (Гейне) функция  равномерно непрерывна на отрезке равномерно непрерывна на отрезке  , следовательно, существует такое , следовательно, существует такое 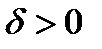 , что для любых , что для любых  , для которых , для которых  , будет , будет 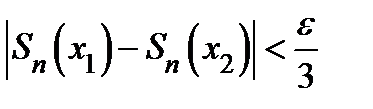 . Поэтому . Поэтому  будет будет
| 
|
 .
.
Отсюда следует равномерная непрерывность функции 
 .
.
Следствие. (О непрерывности суммы ряда). Если все члены ряда непрерывны  и ряд равномерно сходится на этом отрезке, то сумма ряда также непрерывна
и ряд равномерно сходится на этом отрезке, то сумма ряда также непрерывна  .
.
Теорема 2. (О почленном интегрировании последовательностей). Если последовательность непрерывных на отрезке  функций
функций  равномерно сходится
равномерно сходится 
 , то, предел интеграла
, то, предел интеграла 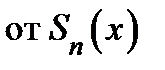 равен интегралу от предела, точнее,
равен интегралу от предела, точнее,
 Ã
à  на отрезке
на отрезке 
 .
.
Доказательство. Утверждение теоремы следует из оценки
 .
.
Следствие. (О почленном интегрировании рядов). Если все члены ряда непрерывны  и ряд равномерно сходится на этом отрезке, то этот ряд можно почленно проинтегрировать по отрезку
и ряд равномерно сходится на этом отрезке, то этот ряд можно почленно проинтегрировать по отрезку  ,
,  .
.
Теорема 2. (О почленном дифференцировании последовательностей). Пусть выполнены следующие условия:
- все функции
 непрерывно дифференцируемы
непрерывно дифференцируемы  ,
, - последовательность функций
 равномерно сходится
равномерно сходится 
 ,
, - числовая последовательность
 сходится.
сходится.
В таком случае последовательность  тоже равномерно сходится к функции
тоже равномерно сходится к функции  , при этом
, при этом  , т.е. производная предела равна пределу производной.
, т.е. производная предела равна пределу производной.
Доказательство. Из теоремы 2. и тождества  следует равномерная сходимость последовательности
следует равномерная сходимость последовательности 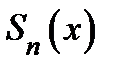 и равенство
и равенство  .
.
Теорема 1. показывает, что функция 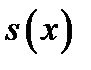 непрерывна
непрерывна  , поэтому, дифференцируя последнее равенство, видим, что
, поэтому, дифференцируя последнее равенство, видим, что  и что
и что  .
.
Следствие. (О почленном дифференцировании рядов). Рассмотрим функциональный ряд  . Пусть все
. Пусть все  − непрерывно дифференцируемые
− непрерывно дифференцируемые  функции, пусть ещё ряд из производных равномерно сходится
функции, пусть ещё ряд из производных равномерно сходится  , а сам ряд сходится в точке
, а сам ряд сходится в точке 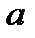 . В таком случае данный ряд равномерно сходится
. В таком случае данный ряд равномерно сходится  , его сумма принадлежит классу
, его сумма принадлежит классу  . Кроме того, этот ряд допускает почленное дифференцирование, т.е. производная суммы ряда равна сумме производных его членов
. Кроме того, этот ряд допускает почленное дифференцирование, т.е. производная суммы ряда равна сумме производных его членов  .
.
 2018-02-13
2018-02-13 523
523








