2018-02-13
250
ЛИТЕРАТУРА: [5],ч.1, гл.6,§ 2,п.2; [6] п. 22.5
Формула интегрирования по частям имеет вид:
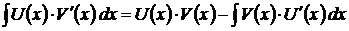
или
Рассмотрим основные случаи использования метода интегрирования по частям.
1). При вычислении интегралов вида:
где 
многочлен, полагаем 
dx 
единицу меньше степени многочлена 
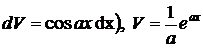. Причем формулу интегрирования по частям используем столько раз, какова степень многочлена 
Пример 1. Найти 
Решение. Положим 
используя формулу интегрирования по частям получаем:
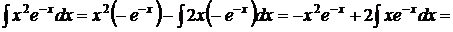
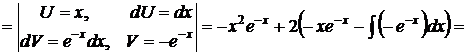
2). При вычислении интегралов вида:
где многочлен, полагаем 
а оставшийся сомножитель в подынтегральной функции - U.
Пример 2. Найти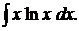 
Решение. Положим 
и получаем:
3). Если вычисляются интегралы вида:
то 
и формулу интегрирования по частям применяем дважды.
Пример3. Найти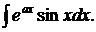 
Решение. Положим 
и получаем:
Заметим, что в последнем выражении получен исходный интеграл, т.е.
Решаем полученное уравнение относительно интеграла:
Задачи:
Найти интегралы:
1). 
| 2). 
|
3). 
| 4). 
|
5). 
| 6). 
|
7). 
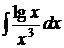
| 8). 
|
9). 
| 10).  
|
11). 
| 12). 
|
13). 
| 14). 
|
15). 
| 16). 
|
17). 
| 18). 
|
19). 
| 20).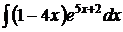 
|
Простейшие интегралы, содержащие квадратный трехчлен
|
|
|
ЛИТЕРАТУРА: [6] п. 24.1-24.2
При нахождении интегралов, содержащих квадратный трехчлен, необходимо выделить полный квадрат в квадратном трехчлене, а затем использовать описанные выше методы интегрирования.
Пример 1. Найти 
Решение. Выделим полный квадрат:
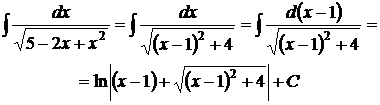
Пример 2. Найти 
Решение. Выделим полный квадрат:
Имеем
Интегралы вида 
решаются с помощью подстановки 
и, после преобразований, приводятся к интегралам от квадратного трехчлена.
Пример 3. Найти 
Решение. Делаем замену переменной 
, тогда
.
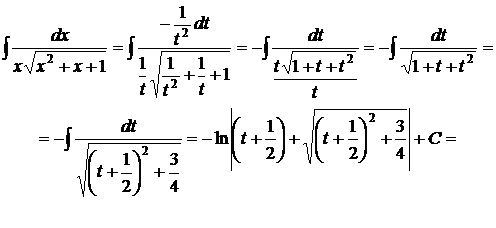
Задачи:
Найти интегралы:
1). 
| 2). 
|
3). 
| 4). 
|
5). 
| 6). 
|
7). 
| 8).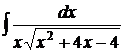 
|
9). 
| 10).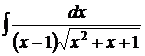 
|
11).  
| 12). 
|
