Замена переменной в неопределенном интеграле

ЛИТЕРАТУРА: [5],ч.1, гл.6,§ 2, п.1; [6] п. 22.4

 

Одним из основных методов интегрирования является метод замены переменной.

1). Полагая 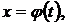где t – новая переменная, дифференцируемая функция, будем иметь

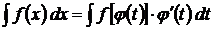
Функцию  стараются выбрать таким образом, чтобы правая часть формулы приняла более удобный для интегрирования вид. Часто за новую переменную принимается иррациональное выражение или выражение, стоящее в знаменателе.

Пример 1. Найти

Решение. Положим  тогда  Подставляя в исходный интеграл, получим:

 

Пример 2. Найти

Решение. Сделаем замену  тогда  и интеграл имеет вид:

 

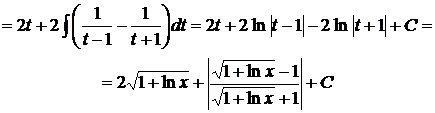
2). К замене переменных также относится метод подведения под знак дифференциала.

Если существует дифференцируемая функция  и функция  такие, что подынтегральное выражение 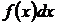 может быть записано в виде

, то вычисление  сводится к вычислению

Пример 3. Найти

Решение. Так как 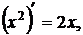 то  и

 

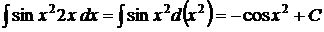
Пример 4. Найти

Решение

 

3). Тригонометрические подстановки.

Если подынтегральная функция содержит выражения  

где > 0, то можно использовать тригонометрические подстановки:

а). , то полагаем  и следовательно

б). , то полагаем

в).  то полагаем

Пример 5. Найти

Решение. Делаем замену , тогда

Задачи:

Найти интегралы:

1).	2).
3).	4).
5).	6).
7).	8).
9).	10).
11).	12).
13).	14).
15).	16).
17).	18).
19).	20).
21).	22).
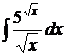
23).	24).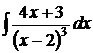
25).	26).
27).	28).
29).