ЛИТЕРАТУРА: [6] п. 26.1 – 26.3
В интегралах вида: 
где m, n – целые числа, используются следующие формулы и приемы:
1). Если  т.е. нечетное положительное число, то
т.е. нечетное положительное число, то
 Аналогично решаются примеры, где n – нечетное положительное число.
Аналогично решаются примеры, где n – нечетное положительное число.
2). Если m, n – четные положительные числа, то используют формулы:

3). Если  целые отрицательные числа одинаковой четности, то
целые отрицательные числа одинаковой четности, то
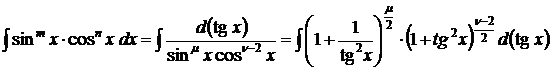 .
.
4). Интегралы вида  приводятся к интегралам от
приводятся к интегралам от  по формулам:
по формулам:
 .
.
5). Интегралы вида  ,
,  ,
,  вычисляются с использованием следующих формул
вычисляются с использованием следующих формул



6). Интегралы вида  где R – рациональная функция, вычисляются с помощью универсальной тригонометрической подстановки
где R – рациональная функция, вычисляются с помощью универсальной тригонометрической подстановки  . Тогда
. Тогда 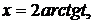

Пример 1. Найти интеграл  .
.
Решение. Так как m = 3 - нечетное положительное число, то применяя выражения  получим интеграл:
получим интеграл:


Пример 2. Найти интеграл 
Решение. Так как m = 3, n = 3 – целые отрицательные числа, то

и интеграл примет вид

Пример 3. Найти интеграл 
Решение. Выполним преобразования:

тогда интеграл равен:

Пример 4. Найти интеграл 
Решение. Делаем подстановку  Тогда
Тогда



Задачи:
Найти интегралы:
1). 
| 2). 
|
3). 
| 4). 
|
5). 
| 6). 
|
7). 
| 8). 
|
9). 
| 10). 
|
11). 
| 12). 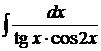
|
13). 
| 14). 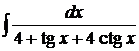
|
15). 
| 16). 
|
Определенный интеграл. Формула Ньютона-Лейбница
ЛИТЕРАТУРА: [5], ч.1, гл.10,§ 7, п.2; [6] п. 27.1, 27.4, 28.1, 29.3.
Геометрически определенный интеграл представляет собой алгебраическую сумму площадей плоских фигур, составляющих криволинейную трапецию, в которой площади частей, расположенных выше оси ОХ, берутся со знаком плюс, а площади частей, расположенных ниже оси ОХ, - со знаком минус.

Если  то справедлива формула Ньютона-Лейбница:
то справедлива формула Ньютона-Лейбница:

Первообразная вычисляется путем нахождения неопределенного интеграла

Пример 1. Вычислить интеграл 
Решение.

Пример 2. Вычислить интеграл 
Решение. Так как  то интеграл
то интеграл

Задачи:
Найти интегралы:
1). 
| 2). 
|
3). 
| 4). 
|
5). 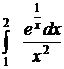
| 6). 
|
7). 
| 8). 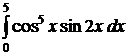
|
9). 
| 10). 
|
 2018-02-13
2018-02-13 237
237








