2018-02-13
974
Визначити розміри поперечних перерізів на кожній ділянці з умови міцності, якщо перша ділянка має круглий переріз, друга –квадратний і третя прямокутний з відношенням сторін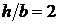 
, при цьому прямокутний переріз розташувати раціонально (табл. 6.1, рис. 6.1). Довжина всіх ділянок 
, коефіцієнт запасу міцності прийняти 
.
Таблиця 6.1. Варіанти завдань до задачі 6
| Варіант | 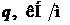 |  |  | Матеріал |
| 0 | 10 |  |  | Сталь 10 |
| 1 | 15 |  |  | Сталь 20 |
| 0 | 20 | 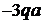 |  | Сталь 20 |
| 3 | 10 |  | | Сталь 40 |
| 4 | −10 |  |  | Сталь 50 |
| 5 | −20 | |  | Сталь 60 |
| 6 | −15 | |  | Сталь 10 |
| 7 | 10 |  | | Сталь 20 |
| 8 | 30 |  | | Сталь 30 |
| 9 | 5 | | | Сталь 40 |
План розв’язування задачі
1. Побудувати розрахункову схему.
2. Побудувати епюри внутрішніх силових факторів на кожній ділянці.
3. Визначити небезпечні перерізи послідовно на кожній ділянці.
4. Знайти небезпечні точки в небезпечних перерізах.
5. Визначити напружений стан в небезпечних точках.
6. Користуючись відповідними критеріями міцності, обчислити розрахункові напруження в небезпечних точках і з умови міцності визначити розміри перерізу.
Розв’язання задачі
Дано (рис. 6.2): , матеріал - Ст3,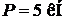 
, 
, 
, .
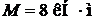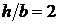1. Побудуємо епюри (рис. 6.3).
2. Розглянемо перший (вертикальний) стержень (рис. 6.4). Він круглого поперечного перерізу. З розрахунку на міцність отримаємо допустиме значення діаметра круглого стержня.
;
.
Візьмемо 
.
3. Розглянемо перший (горизонтальний) стержень (рис. 6.4, де у замінити на z, а всі х – на у). Він також круглого поперечного перерізу. Розрахуємо його аналогічно попередньому стержню:
;
.
Візьмемо 
.
4. Розглянемо другий стержень (рис. 6.5). Він квадратного поперечного перерізу.
;
.
| |
: 
.
Візьмемо 
.
;
;
.
5. Розглянемо третій стержень (рис. 6.6). Він прямокутного поперечного перерізу.
.
Визначимо розміри перерізу без врахування N:
; 
.
.
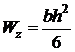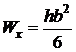
Візьмемо 
, 
.
Перевіримо точку 1 (див. рис. 6.6):
.
Перевіримо точку 2 (див. рис. 6.6):
;
;
.
Перевіримо точку 3 (див. рис. 6.6):
;
;
.
Задача 7
