2018-02-13
354
Определение. Линейным однородным дифференциальным уравнением называется уравнение вида
,
где 
– действительные (вещественные) постоянные.
Особенность этого уравнения: искомая функция 
и ее производные входят в уравнение в первой степени, не перемножаясь между собой.
Определение. Характеристическое уравнение, соответствующее однородному дифференциальному уравнению 
-го порядка имеет вид
| (1) |
и получается из исходного уравнения следующим образом: где коэффициенты 
сохраняются, заменяется единицей, а все ее производные заменяются соответствующими степенями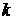 
.
Определение. Система функций 
называется линейно зависимой на отрезке 
, если существуют постоянные 
, не все равные нулю и такие, что имеет место тождество
.
Если же тождество имеет место только при 
, то данные функции линейно независимыми на отрезке .
Определение. Вронскиан системы функций имеет вид
.
Определение. Совокупность линейно независимых частных решений линейного однородного дифференциального уравнения 
определяет фундаментальную систему решений на , если ни в одной точке этого отрезка вронскиан не обращается в нуль, т. е. 
на отрезке .
|
|
|
Способ решения. Общее решение линейного однородного уравнения -го порядка имеет вид 
, где вид зависит от корней характеристического уравнения.
При этом:
1) каждому вещественному корню 
уравнения (1) кратности 
соответствуют частных решений 
;
2) каждой паре комплексно-сопряженных корней 
уравнения (1) кратности соответствуют пар частных решений:
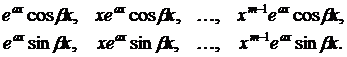
Этих частных решений будет ровно столько, какова степень характеристического уравнения (т.е. столько, каков порядок данного линейного дифференциального уравнения).
Пример 1. Решить уравнение 
.
Решение:
1) Запишем характеристическое уравнение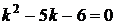 
. Решим его.
, 
, следовательно, уравнение имеет два различных вещественных корня:
, 
, 
, 
.
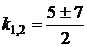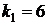2) Найдем частные решения исходного уравнения, соответствующие найденным корням.
Корню 
кратности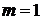 
соответствует одно частное решение 
, корню 
кратности 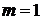соответствует тоже одно частное решение 
.
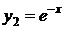3) Тогда общее решение уравнения имеет вид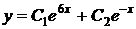 
, где 
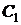и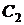 
– произвольные постоянные.
Ответ: Общее решение: .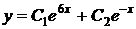
Пример 2. Решить уравнение 
.
Решение:
1) Запишем характеристическое уравнение 
. Решим его.
,
или 
,
, следовательно, уравнение имеет два различных комплексно-сопряженных корня:
.
2) Найдем частные решения исходного уравнения, соответствующие найденным корням.
Корню 
кратности 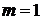соответствует одно частное решение 
, паре комплексно-сопряженных корней 
кратности 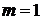соответствует одна пара частных решений: 
, 
.
|
|
|
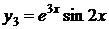3) Тогда общее решение уравнения имеет вид
.
Ответ: Общее решение: .
Пример 3. Найти решение дифференциального уравнения 
, удовлетворяющее начальным условиям 
, 
, 
.
Решение:
1) Запишем характеристическое уравнение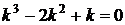 
. Решим его.
, 
,
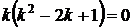или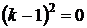 
,
Уравнение имеет один вещественный корень и два вещественных корня 
.
2) Найдем частные решения исходного уравнения, соответствующие найденным корням.
Корню кратности 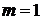соответствует одно частное решение , а корню 
кратности 
соответствуют два частных решения 
и 
.
Тогда общее решение уравнения имеет вид 
или 
.
3) Найдем теперь частное решение уравнения, удовлетворяющее начальным условиям.
Найдем первую и вторую производные
Для нахождения значени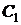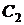й , и 
, удовлетворяющих начальным условиям, получаем систему алгебраических уравнений
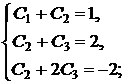
ее решение 
, 
, 
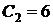. В итоге, получаем частное решение 
.
Ответ: Частное решение: .
Пример 4. Решить уравнение 
.
Решение:
1) Запишем характеристическое уравнение 
. Решим его.
,
или 
(1).
Пусть 
, тогда уравнение (1) примет вид 
(2).
, следовательно, уравнение (2) имеет два одинаковых вещественных корня:
.
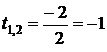Сделав обратную замену, получим
или ,
или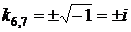 
.
2) Найдем семь частных решений исходного уравнения, соответствующих семи найденным корням.
Корню кратности 
соответствуют три частных решения , 
и 
.
Паре комплексно-сопряженных корней 
кратности соответствуют две пары частных решений: 
, 
и 
, 
.
4) Тогда общее решение уравнения имеет вид
.
Ответ: Общее решение: 
.
