2018-02-13
475
Определение. Уравнение 
(1) называется уравнением в полных дифференциалах, если его левая часть полный дифференциал некоторой функции 
, т.е.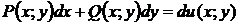 
.
Способ решения. При решении дифференциального уравнения вида (1) сначала проверяем выполнение условия, при котором уравнение (1) является уравнением в полных дифференциалах. Оно состоит в равенстве частных производных 
(2). Затем, используя равенства 
и 
(3), находим функцию . Решение записываем в виде 
.
Замечание. Если 
, то при некоторых условиях существует функция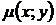 
такая, что 
. Эта функция 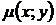называется интегрирующим множителем. Интегрирующий множитель легко найти в случаях:
1) когда 
, тогда 
;
2) когда 
, тогда 
.
Пример. Найти общий интеграл уравнения
.
Решение:
Здесь 
, 
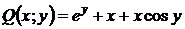. Проверяем выполнение условия (2):
, 
, .
Следовательно, данное уравнение есть уравнение в полных дифференциалах. Условия (3) будут здесь выглядеть как
, 
.
Отсюда имеем
.
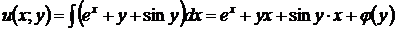Найдем функцию 
, продифференцировав последнее выражение по 
:
.
Получаем уравнение
,
откуда находим 
, т.е. 
. Таким образом, функция 
и общий интеграл уравнения имеет вид
, или 
, где 
.
Ответ: Общий интеграл:
