Рассмотрим три типа дифференциальных уравнений, допускающих понижение порядка.
1) Уравнения вида  .
.
Способ решения. Общее решение получается путем  -кратного интегрирования:
-кратного интегрирования:
 .
.
Пример. Найти общее решение уравнения  .
.
Решение:
Последовательно интегрируя два раза данное уравнение, получим
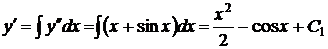 ,
,
 .
.
Ответ: Общее решение:  .
.
2) Уравнения вида  , т.е. уравнения, не содержащие явно искомой функции и ее производных до порядка
, т.е. уравнения, не содержащие явно искомой функции и ее производных до порядка  включительно.
включительно.
На занятиях по высшей математике студентам чаще всего предлагается решать дифференциальные уравнения II порядка. Рассматриваемое уравнение второго порядка имеет вид  , т.е. в этом соотношении явно отсутствует
, т.е. в этом соотношении явно отсутствует  .
.
Способ решения. С помощью замены 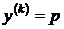 , где
, где 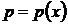 – новая неизвестная функция, порядок уравнения понижается на
– новая неизвестная функция, порядок уравнения понижается на 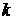 единиц. В частности, для уравнения второго порядка вводится замена
единиц. В частности, для уравнения второго порядка вводится замена  , тогда
, тогда  и уравнение сводится к уравнению первого порядка
и уравнение сводится к уравнению первого порядка  . После его решения необходимо сделать обратную замену и найти общее решение (интеграл) исходного уравнения.
. После его решения необходимо сделать обратную замену и найти общее решение (интеграл) исходного уравнения.
Пример. Найти общее решение уравнения  .
.
Решение:
1) Данное уравнение не содержит явно функцию  . Положим
. Положим  , тогда
, тогда  и уравнение примет вид
и уравнение примет вид
 или или  . .
| (1) |
Это линейное уравнение первого порядка. Решим его методом Лагранжа.
2) Предварительно решаем однородное линейное уравнение, т.е. уравнение  – уравнение первого порядка с разделяющимися переменными.
– уравнение первого порядка с разделяющимися переменными.
 ,
,  ,
,  ,
, 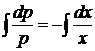 ,
, 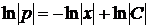 ,
,  .
.
3) Теперь полагаем,  и решение уравнения (1) ищем в виде
и решение уравнения (1) ищем в виде  . Находим производную:
. Находим производную:  . Подставляем значения
. Подставляем значения  и
и  в уравнение (1):
в уравнение (1):
 ,
,  ,
,
 ,
,  ,
,  .
.
4) Подставляя найденное выражение  в искомое общее решение, получим
в искомое общее решение, получим
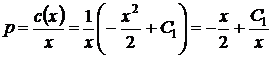 .
.
5) Возвращаясь к исходной переменной, получаем  . Интегрируя это уравнение первого порядка, получаем общее решение исходного уравнения
. Интегрируя это уравнение первого порядка, получаем общее решение исходного уравнения
 .
.
Ответ: Общее решение: 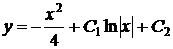 .
.
3) Уравнения вида 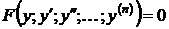 , т.е. уравнения, не содержащие явно независимой переменной
, т.е. уравнения, не содержащие явно независимой переменной 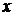 .
.
Рассматриваемое уравнение второго порядка имеет вид  .
.
Способ решения. С помощью замены  , где
, где  – новая неизвестная функция, порядок уравнения понижается на единицу. По правилу дифференцирования сложной функции находим
– новая неизвестная функция, порядок уравнения понижается на единицу. По правилу дифференцирования сложной функции находим
 .
.
Затем найдем
 и т.д.
и т.д.
В частности, уравнение второго порядка  сводится с помощью такой замены к уравнению первого порядка
сводится с помощью такой замены к уравнению первого порядка  . После определения его типа и решения необходимо сделать обратную замену и найти общее решение (интеграл) исходного уравнения.
. После определения его типа и решения необходимо сделать обратную замену и найти общее решение (интеграл) исходного уравнения.
Пример. Решить дифференциальное уравнение 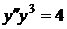 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:  ,
,  .
.
Решение:
1) Данное уравнение не содержит явно переменную 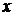 . Положим
. Положим 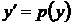 , тогда
, тогда  и уравнение примет вид
и уравнение примет вид  .
.
2) Это дифференциальное уравнение первого порядка с разделяющимися переменными. Разделим переменные:
 .
.
Интегрируем обе части уравнения:
 ,
,  ,
,  ,
,
 .
.
3) Заменяя  на
на  , получаем:
, получаем:  . Поскольку в задаче заданы начальные условия, можно найти постоянную
. Поскольку в задаче заданы начальные условия, можно найти постоянную 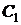 . Так как
. Так как 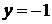 ,
, 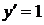 , то
, то
 ,
,  ,
,  и
и  .
.
4) Это дифференциальное уравнение первого порядка с разделяющимися переменными. Решим его.
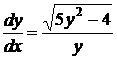 ,
, 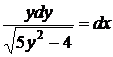 ,
,  (2).
(2).
Вычислим отдельно первый интеграл:
 .
.
Возвращаясь к интегральному уравнению (2), получаем  .
.
5) Найдем теперь постоянную 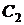 из начального условия
из начального условия  .
.
 ,
,  .
.
В итоге, частный интеграл исходного уравнения
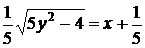 .
.
Ответ: Частный интеграл: 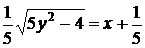 .
.
 2018-02-13
2018-02-13 689
689








