Определение. Линейным неоднородным дифференциальным уравнением называется уравнение вида
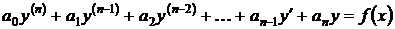 , , | (1) |
где  – действительные (вещественные) постоянные и
– действительные (вещественные) постоянные и 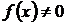 .
.
Способ решения. Общее решение уравнения равно сумме общего решения соответствующего однородного уравнения (при 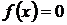 ) и какого-нибудь частного решения исходного неоднородного уравнения, т.е.
) и какого-нибудь частного решения исходного неоднородного уравнения, т.е. 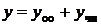 .
.
Для определения какого-либо частного решения данного уравнения рассмотрим два вида правой части, т.е. когда 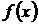 имеет так называемый “специальный вид” (в этом случае не требуется вычислять интегралы) и когда правая часть общего вида (в этом случае решение неоднородного линейного уравнения находится методом Лагранжа – методом вариации произвольных постоянных).
имеет так называемый “специальный вид” (в этом случае не требуется вычислять интегралы) и когда правая часть общего вида (в этом случае решение неоднородного линейного уравнения находится методом Лагранжа – методом вариации произвольных постоянных).
Специальный вид правой части
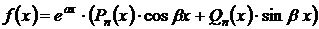 , , | (2) |
где 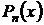 и
и 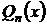 – многочлены
– многочлены  -ой степени.
-ой степени.
В этом случае частное решение 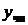 уравнения (1) следует искать в виде
уравнения (1) следует искать в виде
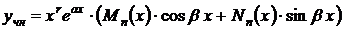 , , | (3) |
где 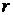 – число, равное кратности
– число, равное кратности 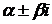 как корня характеристического уравнения,
как корня характеристического уравнения, 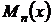 и
и 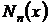 – многочлены степени
– многочлены степени  с неопределенными коэффициентами.
с неопределенными коэффициентами.
После подстановки функции (3) в исходное уравнение (1) находят все неопределенные коэффициенты в искомом частном решении 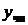 .
.
Замечание. Если правая часть 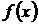 представляет собой сумму функций специального вида
представляет собой сумму функций специального вида 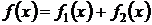 , то частное решение исходного уравнения складывается также из суммы двух частных решений
, то частное решение исходного уравнения складывается также из суммы двух частных решений 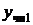 и
и 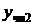 , соответствующих функциям
, соответствующих функциям 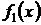 и
и 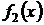 .
.
Пример 1. Решить уравнение 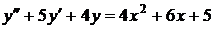 .
.
Решение:
Общее решение уравнения 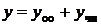 .
.
1) Найдем 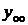 – общее решение соответствующего однородного уравнения:
– общее решение соответствующего однородного уравнения: 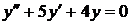 .
.
Запишем характеристическое уравнение 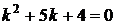 . Решим его.
. Решим его.
 ,
, 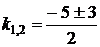 ,
, 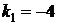 ,
,  .
.
Найдем частные решения уравнения, соответствующие найденным корням: корню 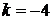 кратности
кратности 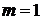 соответствует одно частное решение
соответствует одно частное решение 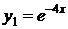 , корню
, корню  кратности
кратности 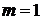 соответствует тоже одно частное решение
соответствует тоже одно частное решение 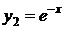 .
.
Тогда общее решение однородного уравнения имеет вид 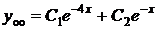 .
.
2) Найдем частное решение исходного неоднородного уравнения 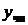 по данной правой части
по данной правой части 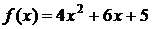 . Она имеет специальный вид (2) с
. Она имеет специальный вид (2) с 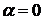 и
и 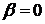 , поэтому
, поэтому 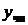 будем искать в виде (3)
будем искать в виде (3)
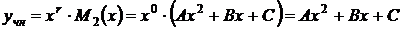 .
.
В данном случае число 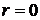 , так как
, так как 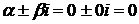 не совпадает с корнями характеристического уравнения.
не совпадает с корнями характеристического уравнения.
Неопределенные коэффициенты А, В и С находим подстановкой частного решения в данное уравнение. Для этого найдем
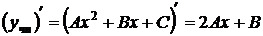 ,
, 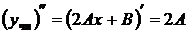 .
.
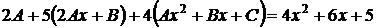 ,
,
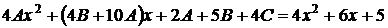 .
.
Приравнивая коэффициенты при одинаковых степенях 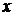 в последнем равенстве, приходим к системе алгебраических уравнений
в последнем равенстве, приходим к системе алгебраических уравнений
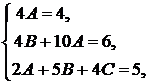
откуда 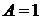 ,
, 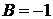 ,
, 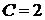 . Следовательно, частное решение
. Следовательно, частное решение 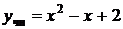 , а общее решение неоднородного уравнения имеет вид
, а общее решение неоднородного уравнения имеет вид
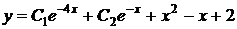 .
.
Ответ: Общее решение: 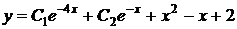 .
.
Пример 2. Решить уравнение 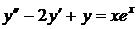 .
.
Решение:
Общее решение уравнения 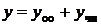 .
.
1) Найдем 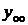 – общее решение соответствующего однородного уравнения:
– общее решение соответствующего однородного уравнения: 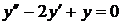 .
.
Запишем характеристическое уравнение 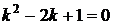 . Решим его.
. Решим его.
 , следовательно, уравнение имеет два одинаковых вещественных корня:
, следовательно, уравнение имеет два одинаковых вещественных корня: 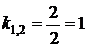 . Корню
. Корню  кратности
кратности  соответствуют два частных решения
соответствуют два частных решения 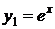 и
и 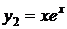 .
.
Тогда общее решение однородного уравнения имеет вид 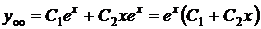 .
.
2) Найдем частное решение исходного неоднородного уравнения 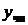 по данной правой части
по данной правой части 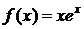 . Она имеет специальный вид (2) с
. Она имеет специальный вид (2) с 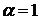 и
и 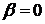 , поэтому
, поэтому 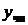 будем искать в виде (3)
будем искать в виде (3)
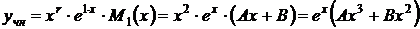 .
.
В данном случае, число 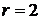 , так как
, так как 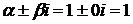 совпадает с двумя корнями характеристического уравнения.
совпадает с двумя корнями характеристического уравнения.
Неопределенные коэффициенты А и В находим подстановкой частного решения в данное уравнение. Для этого найдем
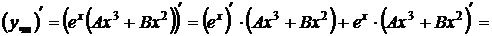
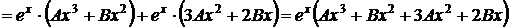 ,
,
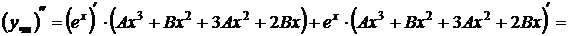
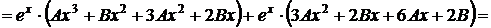
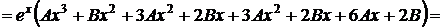
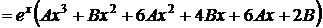 .
.
Подставим 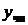 ,
, 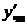 и
и 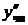 в исходное уравнение
в исходное уравнение 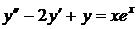 :
:
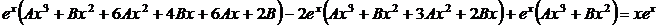 ,
,
 .
.
После сокращения обеих частей уравнения на 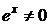 и приведения подобных слагаемых, получим
и приведения подобных слагаемых, получим
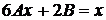 .
.
Приравнивая коэффициенты при одинаковых степенях 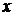 в последнем равенстве, приходим к системе алгебраических уравнений
в последнем равенстве, приходим к системе алгебраических уравнений
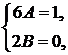
откуда 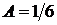 ,
, 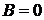 . Следовательно, частное решение
. Следовательно, частное решение 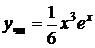 , а общее решение неоднородного уравнения имеет вид
, а общее решение неоднородного уравнения имеет вид 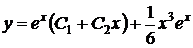 .
.
Ответ: Общее решение: 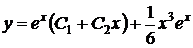 .
.
Пример 3. Решить уравнение 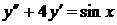 .
.
Решение:
Общее решение уравнения 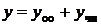 .
.
1) Найдем 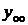 – общее решение соответствующего однородного уравнения:
– общее решение соответствующего однородного уравнения: 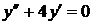 .
.
Запишем характеристическое уравнение 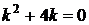 . Решим его.
. Решим его.
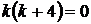 ,
,
 или
или 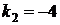 .
.
Найдем частные решения уравнения, соответствующие найденным корням: корню  кратности
кратности 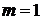 соответствует тоже одно частное решение
соответствует тоже одно частное решение  , корню
, корню 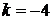 кратности
кратности 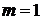 соответствует одно частное решение
соответствует одно частное решение 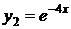 .
.
Тогда общее решение однородного уравнения имеет вид  .
.
2) Найдем частное решение исходного неоднородного уравнения 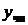 по данной правой части
по данной правой части 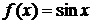 . Она имеет специальный вид (2) с
. Она имеет специальный вид (2) с 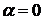 и
и 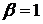 , поэтому
, поэтому 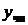 будем искать в виде (3)
будем искать в виде (3)
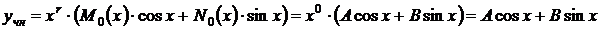 .
.
В данном случае число 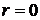 , так как
, так как 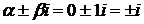 не совпадает с корнями характеристического уравнения.
не совпадает с корнями характеристического уравнения.
Неопределенные коэффициенты А и В находим подстановкой частного решения в данное уравнение. Для этого найдем
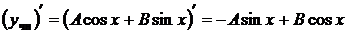 ,
, 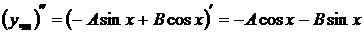 .
.
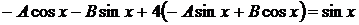 ,
,
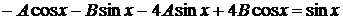 ,
,
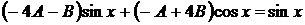 .
.
Приравнивая коэффициенты при 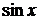 и
и 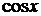 в последнем равенстве, приходим к системе алгебраических уравнений
в последнем равенстве, приходим к системе алгебраических уравнений
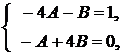
откуда 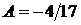 ,
, 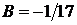 .
.
Следовательно, частное решение 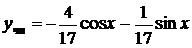 , а общее решение неоднородного уравнения имеет вид
, а общее решение неоднородного уравнения имеет вид
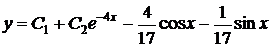 .
.
Ответ: Общее решение: 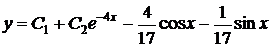 .
.
Рассмотрим общий случай, когда правая часть есть любая функция (в том числе и специальная). В этом случае применяется метод Лагранжа. Покажем его на примере уравнения второго порядка.
Пример 4. Решить уравнение 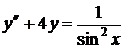 .
.
Решение:
В данном уравнении функция 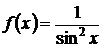 не имеет специальный вид (2).
не имеет специальный вид (2).
1) Сначала находим общее решение 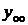 соответствующего однородного уравнения:
соответствующего однородного уравнения: 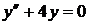 .
.
Запишем характеристическое уравнение 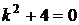 . Решим его.
. Решим его.
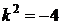 ,
, 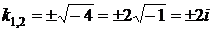 .
.
Паре комплексно-сопряженных корней 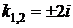 кратности
кратности 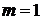 соответствует пара частных решений:
соответствует пара частных решений:
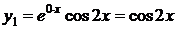 ,
, 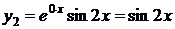 .
.
Тогда общее решение однородного уравнения имеет вид
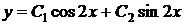 .
.
2) Общее решение исходного неоднородного уравнения ищем в виде 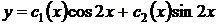 , где
, где 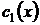 и
и 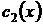 находим из следующей системы уравнений:
находим из следующей системы уравнений:
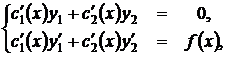
где 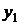 и
и 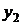 – линейно независимые решения однородного уравнения. В данной задаче эта система имеет вид
– линейно независимые решения однородного уравнения. В данной задаче эта система имеет вид
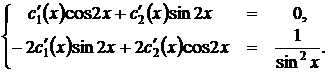
Решим ее. Выразим 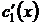 из первого уравнения и подставим по второе:
из первого уравнения и подставим по второе:
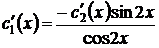 ,
, 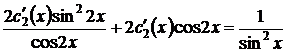 ,
,
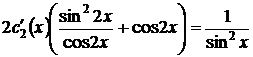 ,
,  ,
,
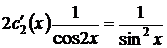 ,
, 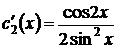 , т.е.
, т.е. 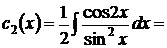
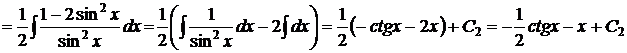 .
.
Найдем теперь 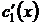 , а затем и
, а затем и 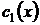 :
:
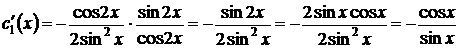 , т.е.
, т.е. 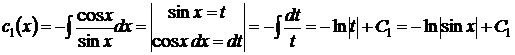 .
.
В итоге, общее решение данного уравнения записывается так:
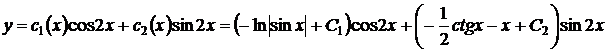 .
.
Ответ: Общее решение: 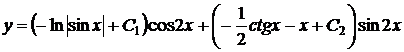 .
.
 2018-02-13
2018-02-13 1525
1525
