
Найдем общее решение системы в виде:
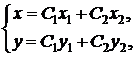
здесь  – неизвестные пока функции,
– неизвестные пока функции,  – произвольные постоянные.
– произвольные постоянные.
Будем искать искомые функции  в виде
в виде  ,
,  . Тогда
. Тогда  ,
,  . Подставим x, y и их производные в систему:
. Подставим x, y и их производные в систему:

или, сокращая на 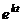 :
:
 | (*) |
Запишем характеристическое уравнение системы:
 или
или 
Находим корни квадратного уравнения:  .
.
При  система (*) примет вид
система (*) примет вид
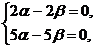
Или 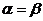 . Пусть
. Пусть  , тогда
, тогда  . Получим частные решения:
. Получим частные решения:

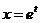 ,
,  .
.
При 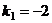 система (*) примет вид
система (*) примет вид

Или 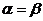 . Пусть
. Пусть  , тогда
, тогда  . Получим частные решения:
. Получим частные решения:

 ,
, 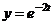 .
.
В итоге, решение системы имеет вид 
Ответ: Общее решение системы 
Контрольная работа
Вариант 1. Решить уравнения: 1.  . 2. . 2.  . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5.  . 6. . 6. 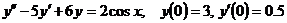 . . | Вариант 2. Решить уравнения: 1.  . 2. . 2.  . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5.  . 6. . 6.  . . |
Вариант 3. Решить уравнения: 1. 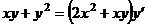 . 2. . 2.  . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5.  . 6. . 6.  . . | Вариант 4. Решить уравнения: 1.  . 2. . 2. 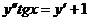 . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5. 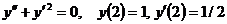 . 6. . 6.  . . |
Вариант 5. Решить уравнения: 1. 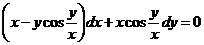 . 2. . 2. 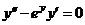 . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5.  . 6. . 6.  . . | Вариант 6. Решить уравнения: 1.  . 2. . 2.  . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5.. . 5..  . 6. . 6. 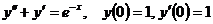 . . |
Вариант 7. Решить уравнения: 1..  . 2. . 2.  . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5.  . 6. . 6.  . . | Вариант 8. Решить уравнения: 1.  . 2. . 2.  . 3. . 3. 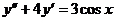 . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5.  . 6. . 6.  . . |
Вариант 9. Решить уравнения: 1. 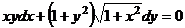 . 2. . 2.  . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4. 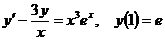 . 5. . 5.  . 6. . 6.  . . | Вариант 10. Решить уравнения: 1.  . 2. . 2.  . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5. 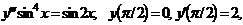  6. 6.  . . |
Вариант 11. Решить уравнения: 1.  . 2. . 2.  . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5.  . 6. . 6.  . . | Вариант 12. Решить уравнения: 1.  . 2. . 2.  . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5.  . 6. . 6.  . . |
Вариант 13. Решить уравнения: 1. 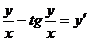 . 2. . 2.  . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5.  . 6. . 6.  . . | Вариант 14. Решить уравнения: 1.  . 2. . 2.  . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5.  . 6. . 6.  . . |
Вариант 15. Решить уравнения: 1.  . 2. . 2.  . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5.  . 6. . 6.  . . | Вариант 16. Решить уравнения: 1. 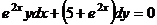 . 2. . 2.  . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5.  . 6. . 6.  . . |
Вариант 17. Решить уравнения: 1.  . 2. . 2. 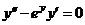 . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5.  . 6. . 6.  . . | Вариант 18. Решить уравнения: 1.  . 2. . 2. 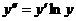 . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5. 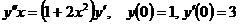 . 6. . 6.  . . |
Вариант 19. Решить уравнения: 1.  . 2. . 2.  . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5.   6. 6.  . . | Вариант 20. Решить уравнения: 1.  . 2. . 2.  . 3. . 3.  . Решить задачи Коши: 4. . Решить задачи Коши: 4.  . 5. . 5.  . 6. . 6.  . . |
Типовой расчет
| Вариант 1 | Вариант 2 | ||||||
1.  | 1. | ||||||
2.  | 2. | ||||||
3.  | 3. | ||||||
4.  | 4. | ||||||
5. 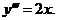 | 5. | ||||||
6. 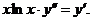 | 6. | ||||||
7.  | 7. | ||||||
8.  | 8. | ||||||
9.  | 9. | ||||||
10.  . . | 10. | ||||||
11.  . . | 11. | ||||||
12. 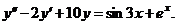 | 12. | ||||||
13.  . . | 13. | ||||||
14.   | 14. | ||||||
15.  | 15. | ||||||
| 16. Найти линию, у которой любая касательная пересекается с осью ординат в точке, одинаково удаленной от точки касания и от начала координат. | 16. Найти линию, у которой начальная ордината любой касательной на две единицы масштаба меньше абсциссы точки касания. | ||||||
| Вариант 3 | Вариант 4 | ||||||
1.  | 1. | ||||||
2.  | 2. | ||||||
3. 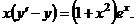 | 3. | ||||||
4.  | 4. | ||||||
5.  | 5. | ||||||
6. 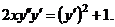 | 6. | ||||||
7.  | 7. | ||||||
8.  . . | 8. | ||||||
9.  . . | 9. | ||||||
10.  | 10. | ||||||
11.  . . | 11. | ||||||
12.  . . | 12. | ||||||
13.  . . | 13. | ||||||
14.   | 14. | ||||||
15.  | 15. | ||||||
| 16. Найти линию, у которой квадрат длины отрезка, отсекаемого любой касательной от оси ординат, равен произведению координат точки касания. | 16. Найти линию, у которой длина нормали есть постоянная величина a. | ||||||
| Вариант 5 | Вариант 6 | ||||||
1.  | 1. | ||||||
2.  | 2. | ||||||
3.  | 3. | ||||||
4. 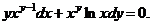 | 4. | ||||||
5.  | 5. | ||||||
6. 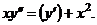 | 6. | ||||||
7.  | 7. | ||||||
8.  | 8. | ||||||
9.  . . | 9. | ||||||
10.  . . | 10. | ||||||
11.  . . | 11. | ||||||
12.  | 12. | ||||||
13.  . . | 13. | ||||||
14.   | 14. | ||||||
15. 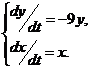 | 15. | ||||||
16. Найти линию, проходящую через точку  и имеющую постоянную касательную, равную а. и имеющую постоянную касательную, равную а. | 16. Найти линию, у которой длина нормали в любой ее точке равна расстоянию от этой точки от начала координат. | ||||||
| Вариант 7 | Вариант 8 | ||||||
1.  | 1. | ||||||
2.  | 2. | ||||||
3.  | 3. | ||||||
4.  | 4. | ||||||
5. 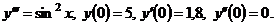 | 5. | ||||||
6.  | 6. | ||||||
7. 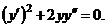 | 7. | ||||||
8.  | 8. | ||||||
9.  . . | 9. | ||||||
10.  . . | 10. | ||||||
11.  | 11. | ||||||
12.  | 12. | ||||||
13.  . . | 13. | ||||||
14.   | 14. | ||||||
15.  | 15. | ||||||
| 16. Найти кривую, проходящую через точку (0;1), у которой подкасательная равна сумме координат точки касания. | 16. Найти уравнение кривой, у которой длина отрезка, отсекаемого касательной на оси ординат равна поднормали. | ||||||
| Вариант 9 | Вариант 10 | ||||||
1.  | 1. | ||||||
2.  | 2. | ||||||
3.  | 3. | ||||||
4.  | 4. | ||||||
5.  | 5. | ||||||
6.  | 6. | ||||||
7.  | 7. | ||||||
8.  | 8. | ||||||
9. 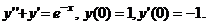 | 9. | ||||||
10.  . . | 10. | ||||||
11.  . . | 11. | ||||||
12. 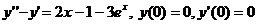 . . | 12. | ||||||
13.  | 13. | ||||||
14.  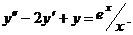 | 14. | ||||||
15.  | 15. | ||||||
| 16. Найти уравнение кривой, у которой длина отрезка, отсекаемого касательной на оси абсцисс, равна квадрату ординаты точки касания. | 16. Найти линию, у которой начальная ордината любой касательной равна соответствующей поднормали. | ||||||
| Вариант 11 | Вариант 12 | ||||||
1.  | 1. | ||||||
2.  | 2. | ||||||
3.  | 3. | ||||||
4.  | 4. | ||||||
5.  | 5. | ||||||
6.  | 6. | ||||||
7. 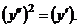 | 7. | ||||||
8.  , ,  . . | 8. | ||||||
9.   | 9. | ||||||
10.  . . | 10. | ||||||
11.  . . | 11. | ||||||
12.  . . | 12. | ||||||
13.  . . | 13. | ||||||
14.   | 14. | ||||||
15. 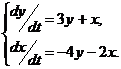 | 15. | ||||||
| 16. Найти линию, проходящую через точку (2,3) и обладающую тем свойством, что отрезок любой ее касательной, заключенный между координатными осями, делится точкой касания пополам. | 16. Найти кривую, для которой отрезок на оси ординат, отсекаемый любой касательной, равен абсциссе точки касания. | ||||||
| Вариант 13 | Вариант 14 | ||||||
| 1. | 1. | ||||||
| 2. | 2. | ||||||
| 3. | 3. | ||||||
| 4. | 4. | ||||||
| 5. | 5. | ||||||
| 6. | 6. | ||||||
| 7. | 7. | ||||||
| 8. | 8. | ||||||
| 9. | 9. | ||||||
| 10. | 10. | ||||||
| 11. | 11. | ||||||
| 12. | 12. | ||||||
| 13. | 13. | ||||||
| 14. | 14. | ||||||
| 15. | 15. | ||||||
| 16. Найти уравнение кривой, у которой подкасательная равна среднему арифметическому координат точки касания. | 16. Найти уравнение кривой, проходящей через точку (3;1), для которой отрезок касательной между точкой касания и осью ОХ делится пополам в точке пересечения с осью ОУ. | ||||||
| Вариант 15 | Вариант 16 | ||||||
| 1. | 1. | ||||||
| 2. | 2. | ||||||
| 3. | 3. | ||||||
| 4. | 4. | ||||||
| 5. | 5. | ||||||
| 6. | 6. | ||||||
| 7. | 7. | ||||||
| 8. | 8. | ||||||
| 9. | 9. | ||||||
| 10. | 10. | ||||||
| 11. | 11. | ||||||
| 12. | 12. | ||||||
| 13. | 13. | ||||||
| 14. | 14. | ||||||
| 15. | 15. | ||||||
| 16. Найти кривую, у которой подкасательная вдвое больше абсциссы точки касания. | 16. Найти линию, у которой квадрат длины отрезка, отсекаемого любой касательной от оси ординат, равен произведению координат точки касания. | ||||||
| Вариант 17 | Вариант 18 | ||||||
| 1. | 1. | ||||||
| 2. | 2. | ||||||
| 3. | 3. | ||||||
| 4. | 4.. | ||||||
| 5. | 5. | ||||||
| 6. | 6. | ||||||
| 7. | 7. | ||||||
| 8. | 8. | ||||||
| 9. | 9. | ||||||
| 10. | 10. | ||||||
| 11. | 11. | ||||||
| 12. | 12. | ||||||
| 13. | 13. | ||||||
| 14. | 14. | ||||||
| 15. | 15. | ||||||
| 16. Найти линию, у которой начальная ордината любой касательной на две единицы масштаба меньше абсциссы точки касания. | 16. Найти линию, у которой любая касательная пересекается с осью ординат в точке, одинаково удаленной от точки касания и от начала координат. | ||||||
| Вариант 19 | Вариант 20 | ||||||
| 1. | 1. | ||||||
| 2. | 2. | ||||||
| 3. | 3. | ||||||
| 4. | 4. | ||||||
| 5. | 5. | ||||||
| 6. | 6. | ||||||
| 7. | 7. | ||||||
| 8. | 8. | ||||||
| 9. | 9. | ||||||
| 10. | 10. | ||||||
| 11. | 11. | ||||||
| 12. | 12. | ||||||
| 13. | 13. | ||||||
| 14.
Подборка статей по вашей теме:
| |||||||
 2018-02-13
2018-02-13 1212
1212




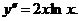



 .
. .
.

 .
.








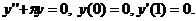
 .
.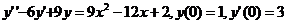 .
.
 .
. .
.









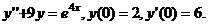
 .
. .
.
 .
.






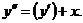

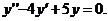

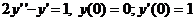 .
. .
. .
. .
.





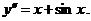




 .
.
 .
. .
.








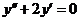 ,
, 
 .
.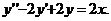
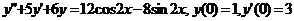
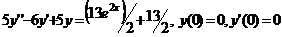 .
.



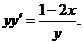



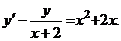

 , (интегрирующий множитель
, (интегрирующий множитель  )
)



 .
.
 .
.
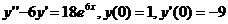 .
. .
.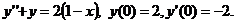

 .
. .
. .
.
 .
. .
.

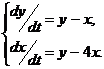


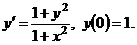




 .
. , (интегрирующий множитель
, (интегрирующий множитель  )
)



 .
. .
.
 .
.

 .
.
 .
. .
. .
. .
.











 , (интегрирующий множитель
, (интегрирующий множитель  )
)




 .
. .
. .
. .
. .
. .
.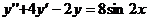 .
. .
. .
. .
. .
.



 .
. .
.




 , (интегрирующий множитель
, (интегрирующий множитель  )
)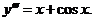
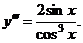
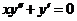 .
.

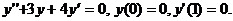

 .
. .
. .
. .
.
 .
. .
. .
. .
. .
. .
.