Системы линейных дифференциальных уравнений с постоянными коэффициентами

Определение. Система дифференциальных уравнений вида

(1)

где – неизвестные функции независимой переменной t, называется нормальной системой.

Если правые части нормальной системы (1) являются линейными функциями относительно , то система дифференциальных уравнений называется линейной.

Ограничимся рассмотрением линейных систем дифференциальных уравнений с постоянными коэффициентами:

Способ решения. Один из методов решения заключается в сведении системы к линейному однородному дифференциальному уравнению -го порядка с постоянными коэффициентами. Это может быть достигнуто дифференцированием одного из уравнений системы и исключением всех неизвестных, кроме одной.

Второй способ состоит в нахождении общего решения системы с помощью характеристического уравнения системы. Покажем этот способ на примере системы, характеристическое уравнение которой имеет различные вещественные корни.

Пример 1. Решить систему .

Решение:

Первый способ. Метод исключения.

Дифференцируя обе части первого уравнения по независимой переменной 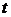, получим . Далее заменим выражением из второго уравнения:

или , .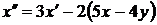

Теперь заменим выражением из первого уравнения (1):

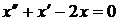, , (2).

Полученное уравнение является однородным линейным уравнением второго порядка с постоянными коэффициентами. Решим его.

Запишем характеристическое уравнение .

, , , .

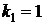Найдем частные решения уравнения, соответствующие найденным корням: корню кратности 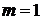соответствует одно частное решение , корню кратности 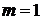соответствует тоже одно частное решение .