Это уравнение линейное относительно  и
и  . Положим
. Положим  , где
, где  и
и  – вспомогательные искомые функции. Заметим, что если
– вспомогательные искомые функции. Заметим, что если  , то один из множителей (
, то один из множителей ( или
или  ) можно выбрать произвольно (но не равным нулю). Тогда
) можно выбрать произвольно (но не равным нулю). Тогда  и уравнение примет вид
и уравнение примет вид
 .
.
Раскроем скобки и сгруппируем члены, содержащие  :
:
 , ,  . . | (1) |
Выберем функцию  таким образом, чтобы скобка в (1) обращалась в нуль. Тогда уравнение равносильно следующей системе:
таким образом, чтобы скобка в (1) обращалась в нуль. Тогда уравнение равносильно следующей системе:
 | (2) (3) |
Уравнение (2) – дифференциальное уравнение с разделяющимися переменными. Решим его.
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
(берем простейшее частное решение этого уравнения, считая произвольную постоянную С, возникающую при взятии интеграла, равной нулю).
Подставляем найденное значение  в уравнение (3). Имеем
в уравнение (3). Имеем
 ,
,  .
.
Интегрируя, находим
 .
.
Окончательно, общее решение исходного уравнения
 .
.
Ответ: Общее решение: 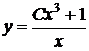 .
.
Второй способ. Метод Лагранжа.
Предварительно решаем однородное линейное уравнение, т.е. уравнение  – уравнение первого порядка с разделяющимися переменными.
– уравнение первого порядка с разделяющимися переменными.
 ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Метод вариации произвольной постоянной состоит в том, что постоянную С в полученном решении заменяем функцией  , т.е. полагаем
, т.е. полагаем  и решение исходного уравнения ищем в виде
и решение исходного уравнения ищем в виде 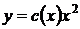 .
.
Находим производную:  . Подставляем значения
. Подставляем значения  и
и  в исходное уравнение:
в исходное уравнение:
 ,
,  ,
,
 ,
,  ,
,  .
.
Подставляя найденное выражение  в искомое общее решение, получим
в искомое общее решение, получим
 .
.
Естественно, такое же решение было получено методом Бернулли.
Уравнение Бернулли
Определение. Дифференциальное уравнение вида  ,
,  ,
,  ,
,  (или
(или  ) называется уравнением Бернулли.
) называется уравнением Бернулли.
Если  , то уравнение линейное, а при
, то уравнение линейное, а при  – с разделяющимися переменными.
– с разделяющимися переменными.
Способ решения. Подстановка  сводит уравнение Бернулли к линейному уравнению, и поэтому его можно решать как линейное дифференциальное уравнение первого порядка, т.е. подстановкой
сводит уравнение Бернулли к линейному уравнению, и поэтому его можно решать как линейное дифференциальное уравнение первого порядка, т.е. подстановкой  или методом вариации произвольной постоянной. Но на практике уравнение Бернулли удобнее решать подстановкой
или методом вариации произвольной постоянной. Но на практике уравнение Бернулли удобнее решать подстановкой  сразу же, без сведения его к линейному.
сразу же, без сведения его к линейному.
Пример. Найти частное решение уравнения  , удовлетворяющее заданному начальному условию
, удовлетворяющее заданному начальному условию  .
.
Решение:
Данное уравнение является уравнением Бернулли ( ). Положим
). Положим  ,
,  и уравнение примет вид
и уравнение примет вид
 .
.
Сгруппируем члены, содержащие  :
:
 . . | (1) |
Уравнение (1) равносильно следующей системе:
 | (2) (3) |
Решим уравнение (2) – дифференциальное уравнение с разделяющимися переменными.
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Подставляем найденное значение  в уравнение (3). Имеем,
в уравнение (3). Имеем,  ,
,  – уравнение с разделяющимися переменными. Решим его.
– уравнение с разделяющимися переменными. Решим его.
 ,
,  ,
,  ,
, 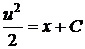 ,
,  ,
,  .
.
Окончательно, общее решение исходного уравнения
 .
.
Найдем частное решение, которое удовлетворяет заданному начальному условию, т.е. при  значение
значение  . Подставив в общее решение, получим
. Подставив в общее решение, получим
 ,
, 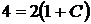 ,
,  ,
,  .
.
Следовательно, искомое частное решение  .
.
Ответ: Частное решение:  .
.
 2018-02-13
2018-02-13 1174
1174
