Оценка параметров уравнения множественной регрессии

Параметры уравнения множественной регрессии оценивают­, как и в парной регрессии, методом наименьших квадратов (МНК). При его применении строят систему нормальных уравнений, решение которой и позволяет получить оценки пара­метров регрессии.

Так, для уравнения (3.1) сис­тема нормальных уравнений имеет вид:

Если разделить обе части уравнений на n, то в качестве коэффициентов системы получим средние значения:

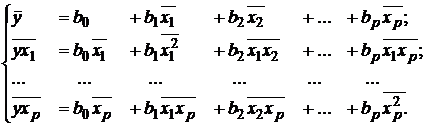
(3.4)

Систему можно решить методом определителей:

,

(3.5)

где – определитель системы

;

(3.6)

, , …, – частные определители, которые получаются путем замены соответствующего столбца в определителе  столбцом левой части системы (3.4), например:

.

В этом частном определителе второй столбец заменен столбцом левой части системы (3.4).

Возможна запись уравнения множе­ственной регрессии в стандарти­зованном масштабе на основе матрицы парных коэффи­циентов корреляции. Тогда уравнение регрессии имеет вид:

,

(3.7)

где , , …, – стандартизованные переменные: , , для которых средние значения равны нулю: , а средние квадратические отклонения равны единице: ; – стандартизованные коэффициенты регрессии.

Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобра­зований получают систему нормальных уравнений вида

(3.8)

Решая ее методом определителей, находят стан­дартизованные коэффициенты регрессии (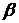 -коэффициенты).

Стандартизованные коэффициенты регрессии показывают, на сколько сигм изменится в среднем результативный фактор у, если соответст­вующий фактор 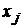 изменится на одну сигму при неизменном среднем уровне других факторов. В силу того, что все перемен­ные заданы как центрированные и нормированные, стандартизо­ванные коэффициенты регрессии  сравнимы между собой. Сравнивая их друг с другом, можно ранжировать факторы по си­ле их воздействия на результативный фактор у. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от ко­эффициентов «чистой» регрессии, которые несравнимы между собой. Коэффициенты «чистой» регрессии 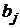 связаны со стандартизованными коэффициентами регрессии :

.

(3.9)

Это позволяет от уравнения регрессии в стандартизованном масштабе

(3.10)

переходить к уравнению регрессии в натуральном масштабе пе­ременных:

.

(3.11)

Параметр  определяют по формуле

.

(3.12)

Стандартизованные коэффициенты регрессии  используют при отсеве факторов 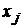. Из модели множественной регрессии исключают факторы с наименьшими значениями . Можно выразить стандартизованный коэффициент регрессии  через коэффициент «чистой» регрессии из формулы (3.9)

.

(3.13)

Для того, чтобы оценить, на сколько процентов (от среднего) изменится в среднем у при увеличении только 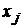 на 1 %, используют средний коэффициент эластичности

.

(3.14)