Для оценки качества построенной модели используют следующие показатели:
· средняя ошибка аппроксимации  – характеризует среднее отклонение расчетных значений
– характеризует среднее отклонение расчетных значений 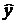 от фактических значений y:
от фактических значений y:
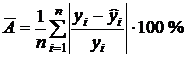 . .
| (2.9) |
Если  не превышает 10%, то качество аппроксимации считают очень хорошим; если
не превышает 10%, то качество аппроксимации считают очень хорошим; если  свыше 10% до 12% – хорошим; если
свыше 10% до 12% – хорошим; если  свыше 12% до 15% – удовлетворительным; если
свыше 12% до 15% – удовлетворительным; если  превышает 15% – неудовлетворительным;
превышает 15% – неудовлетворительным;
· коэффициент (индекс) детерминации 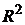 (квадрат коэффициента корреляции для парной линейной регрессии) – характеризует долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у:
(квадрат коэффициента корреляции для парной линейной регрессии) – характеризует долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у:
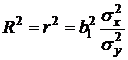 , ,
| (2.10) |
где в числителе записана дисперсия фактора x или дисперсия результативного признака y, обусловленная факторным признаком x, а в знаменателе – общая дисперсия результативного признака y. На основе дисперсионного анализа можно получить другое выражение коэффициента детерминации. Для этого записывают основное уравнение дисперсионного анализа

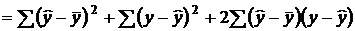 , ,
| (2.11) |
где 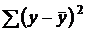 – общая сумма квадратов отклонений;
– общая сумма квадратов отклонений;  – сумма квадратов отклонений, обусловленная регрессией («объяснённая» или «факторная»);
– сумма квадратов отклонений, обусловленная регрессией («объяснённая» или «факторная»); 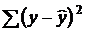 – сумма квадратов отклонений остатков («остаточная»).
– сумма квадратов отклонений остатков («остаточная»).
Можно доказать, что третье слагаемое в формуле (2.11) несущественно отличается от нуля. Тогда коэффициент детерминации можно представить в виде
 . .
| (2.12) |
Заменяя числитель данного уравнения правой частью уравнения регрессии в отклонениях (2.7), можно доказать, что для линейной корреляции 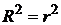 :
:
 ; ;
|
· F-тест – состоит в проверке гипотезы 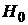 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняют сравнение фактического
о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняют сравнение фактического  и критического (табличного)
и критического (табличного) 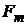 значений F-критерия Фишера.
значений F-критерия Фишера. 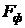 определяют по формуле
определяют по формуле
 . .
| (2.13) |
Таким образом, 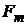 – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости
– это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости  , при котором ещё можно признать статистическую значимость уравнения регрессии. Уровень значимости
, при котором ещё можно признать статистическую значимость уравнения регрессии. Уровень значимости  характеризует вероятность отвергнуть правильную гипотезу при условии, что она верна. Тогда вероятность принятия правильной гипотезы равна
характеризует вероятность отвергнуть правильную гипотезу при условии, что она верна. Тогда вероятность принятия правильной гипотезы равна  . Обычно уровень значимости
. Обычно уровень значимости  принимают равным: 0,01 (1%) – для высокой точности; 0,05 (5%) – для обычной точности; 0,1 (10%) – для низкой точности.
принимают равным: 0,01 (1%) – для высокой точности; 0,05 (5%) – для обычной точности; 0,1 (10%) – для низкой точности.
Если  , то гипотезу
, то гипотезу 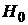 о случайной природе оцениваемых характеристик отклоняют и принимают гипотезу
о случайной природе оцениваемых характеристик отклоняют и принимают гипотезу  об их статистической значимости и надёжности. Если
об их статистической значимости и надёжности. Если  , то гипотезу
, то гипотезу 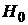 не отклоняют и признают статистическая незначимость, ненадежность уравнения регрессии.
не отклоняют и признают статистическая незначимость, ненадежность уравнения регрессии.
· t-критерий Стъюдента и доверительные интервалы каждого из показателей. Выдвигают гипотезу 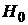 о случайной природе показателей, т. е. о незначимом их отличии от нуля. Оценку значимости параметров уравнения регрессии выполняют с помощью t-статистик или t-критерия Стьюдента путем сопоставления их абсолютных значений с величиной случайной ошибки:
о случайной природе показателей, т. е. о незначимом их отличии от нуля. Оценку значимости параметров уравнения регрессии выполняют с помощью t-статистик или t-критерия Стьюдента путем сопоставления их абсолютных значений с величиной случайной ошибки:
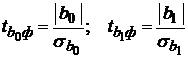 . .
| (2.14) |
Случайные ошибки параметров линейной регрессии определяют по формулам:
 ; ;
| (2.15) | |
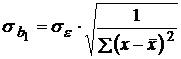 . .
| (2.16) |
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством
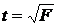 . .
|
Сравнивая фактическое 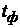 и критическое (табличное)
и критическое (табличное)  значения t-статистик, принимают или отклоняют гипотезу
значения t-статистик, принимают или отклоняют гипотезу 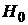 . Если
. Если 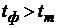 , то гипотезу
, то гипотезу 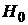 отклоняют и принимают гипотезу
отклоняют и принимают гипотезу 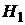 , т. е.
, т. е. 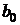 или
или 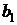 не случайно отличаются от нуля и сформировались под влиянием систематически действующего факторного признака х. В этом случае для соответствующего параметра строят доверительный интервал. Если
не случайно отличаются от нуля и сформировались под влиянием систематически действующего факторного признака х. В этом случае для соответствующего параметра строят доверительный интервал. Если  , то гипотезу
, то гипотезу 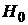 не отклоняют, признают случайную природу формирования
не отклоняют, признают случайную природу формирования 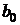 или
или 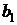 и доверительный интервал не строят.
и доверительный интервал не строят.
Таким образом,  – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости
– это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости  , при котором ещё можно признать статистическую значимость соответствующего параметра уравнения регрессии.
, при котором ещё можно признать статистическую значимость соответствующего параметра уравнения регрессии.
Для расчета доверительных интервалов определяют предельную ошибку  (половину ширины доверительного интервала) для каждого показателя:
(половину ширины доверительного интервала) для каждого показателя:
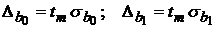 . .
| (2.18) |
Формулы для расчета доверительных интервалов имеют следующий вид:
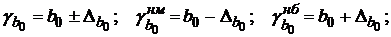
 . .
| (2.19) |
В пределы соответствующего доверительного интервала с вероятностью  попадает фактическое (реальное) значение параметра
попадает фактическое (реальное) значение параметра 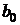 или
или 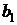 . Если в эти границы попадает нуль, т. е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимают равным нулю, так как он не может одновременно принимать и положительное и отрицательное значения.
. Если в эти границы попадает нуль, т. е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимают равным нулю, так как он не может одновременно принимать и положительное и отрицательное значения.
2.6. Прогнозирование значений результативного признака
с использованием модели линейной регрессии
Различают два вида прогнозных оценок: точечную и интервальную.
Точечную оценку (наиболее вероятное прогнозное значение) 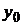 определяют путем подстановки в уравнение регрессии
определяют путем подстановки в уравнение регрессии 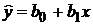 прогнозного значения
прогнозного значения  :
: 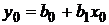 .
.
Интервальные оценки прогноза сами бывают двух видов: для наиболее вероятного (среднего) значения 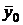 и для индивидуального (отдельного) значения
и для индивидуального (отдельного) значения 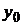 .
.
Интервальная оценка для наиболее вероятного (среднего) значения 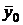 заключается в расчёте доверительного интервала, в который с вероятностью
заключается в расчёте доверительного интервала, в который с вероятностью  попадёт фактическое (реальное) среднее значение
попадёт фактическое (реальное) среднее значение  .
.
При этом вычисляют среднюю стандартную ошибку прогноза по формуле
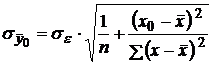 . .
| (2.20) |
Данная формула показывает, что наименьшее значение средней стандартной ошибки прогноза 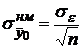 будет при
будет при  . Чем больше разность между
. Чем больше разность между  и
и 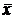 , тем ошибка прогноза больше, шире доверительный интервал и прогноз менее определённый.
, тем ошибка прогноза больше, шире доверительный интервал и прогноз менее определённый.
Затем строят доверительный интервал прогноза для наиболее вероятного (среднего) значения 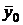 :
:
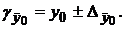
| (2.21) |
Для этого определяют половину ширины этого интервала  , а также его нижнюю
, а также его нижнюю  и верхнюю
и верхнюю 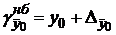 границы. В пределы этих границ с вероятностью
границы. В пределы этих границ с вероятностью  попадёт фактическое (реальное) среднее значение
попадёт фактическое (реальное) среднее значение  .
.
Интервальная оценка для индивидуального (отдельного) значения 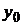 заключается в расчёте доверительного интервала, в который с вероятностью
заключается в расчёте доверительного интервала, в который с вероятностью  попадёт любое индивидуальное (отдельное) значение
попадёт любое индивидуальное (отдельное) значение 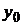 .
.
Для ожидаемого индивидуального (отдельного) значения 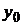 уравнение ошибки прогноза
уравнение ошибки прогноза  имеет вид:
имеет вид:
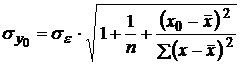 . .
| (2.22) |
Наименьшее значение ошибки прогноза 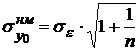 будет при
будет при  .
.
Затем строят доверительный интервал прогноза для индивидуального значения 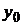 :
:

| (2.23) |
Для этого определяют половину ширины этого интервала  , а также его нижнюю
, а также его нижнюю 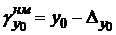 и верхнюю
и верхнюю 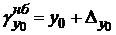 границы. В пределы этих границ с вероятностью
границы. В пределы этих границ с вероятностью  попадёт любое индивидуальное (отдельное) значение
попадёт любое индивидуальное (отдельное) значение 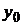 .
.
 2018-02-13
2018-02-13 289
289








