Парная линейная корреляция

Для оценки тесноты связи у и х можно использовать коэффициент 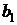, но он зависит от единиц измерения переменных. Поэтому предпочтительнее переходить к безразмерной характеристике, в качестве которой в статистике используют среднее квадратическое отклонение .

Разделив обе части уравнения (2.7) на  и умножив правую часть на , получим новое уравнение

.

В этом уравнении величину

(2.8)

называют линейным коэффи­циентом выборочной парной корреляции. Этот коэффициент показывает, на сколько величин  изменится в среднем у при изменении х на одну величину .

Формула (2.8) показывает, что знак «+» или «–» коэффициента корреляции определяется знаком коэффициента 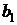, т. к.  и  неотрицательны. Если , то корреляционную связь называют прямой. При этом увеличение одной из переменных ведет к увеличению средней величины другой переменной. Если , то корреляционную связь называют обратной. При этом увеличение одной из переменных ведет к уменьшению средней величины другой переменной.

Коэффициент корреляции обладает следующими свойствами:

1. Для любых процессов или явлений величина коэффициента корреляции находится в интервале , т. е. .

2. При  связь между у и х отсутствует. При этом корреляционное поле имеет форму круга, а линия регрессии располагается горизонтально.

3. При  связь между у и х называют корреляционной. При этом корреляционное поле имеет форму эллипса, а угол наклона линии регрессии острый (но не более 45°), или тупой (но не менее 135°). Каждому значению х соответствует несколько значений у. Чем ближе  к единице, тем меньше интервал этих значений, эллипс корреляционного поля более вытянут вдоль линии регрессии, угол её наклона ближе к 45° (при ) или к 135° (при ), связь между у и х теснее.

Если  связь между у и х считают несущественной; если  связь между у и х считают существенной; если  связь между у и х считают тесной.

4. При , т. е. при  или при  связь между у и х называют линейной функциональной зависимостью. При этом корреляционное поле превращается в линию регрессии, а угол её наклона равен 45° (при ) или 135° (при ). Таким образом, все значения у располагаются на линии регрессии.

В случае нелинейной регрессии тесноту связи у и х оценивают с помощью индекса корреляции :

.

2.4. Основные положения регрессионного анализа.
Теорема Гаусса-Маркова

Основные предпосылки регрессионно­го анализа заключаются в следующем:

1.В модели (2.1) ошибка  (или зависимая переменная ) есть величина случайная, а объясняющая переменная – величина неслучайная.

2.Математическое ожидание ошибки  равно нулю:

(или математическое ожидание зависимой переменной  равно линейной функции регрессии .

3. Дисперсия ошибки  постоянна для любого i:

(или ) – условие гомоскедастичности или равноизменчивости ошибки  (или зависимой переменной ).

4. Ошибки  и  (или переменные.  и ) не коррелированны:

5. Ошибка  (или зависимая переменная ) есть нормаль­но распределенная случайная величина.

В этом случае модель (2.1) называют классической нор­мальной линейной регрессионной моделью (Classical Normal Linear Regression model).

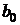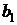Для получения уравнения регрессии достаточно предпосы­лок 1–4. Требование выполнения предпосылки 5 (т. е. рассмот­рение «нормальной регрессии») необходимо для оценки точ­ности уравнения регрессии и его параметров. Оценкой модели (2.1) по выборке является уравнение рег­рессии (2.2). Параметры этого уравнения  и  определяют на основе МНК. Воздействие неучтенных случайных факторов и ошибок на­блюдений в модели (2.1) определяют с помощью дисперсии ошибок или остаточной дисперсии 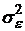. Несмещенной оценкой этой дисперсии является выборочная остаточная дис­персия

.

В математической статистике для получения несмещенной оценки дисперсии случайной величины соответст­вующую сумму квадратов отклонений от среднего значения делят не на число наблюдений n, а на число степеней свободы (degress of free­dom) , равное разности между числом независимых на­блюдений n случайной величины и числом связей m, ограничи­вающих свободу их изменения, т. е. числом m уравнений, связы­вающих эти наблюдения (числом неизвестных параметров в уравнении регрессии) или числом факторных признаков р в уравнении регрессии. Поэтому в знаменателе стоит число степеней свободы , т. к. две степени свободы теряются при определении двух параметров 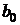 и 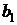 прямой линии регрессии из системы нормальных уравнений (2.4).

Оценк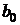и  и 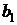 параметров регрессии являются «наилучшими» в соответствии с теоремой Гаусса-Маркова:

Если регрессионная модель (2.1 ) удовлетворяет предпосылкам 1–4, то оценк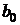и  и 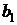  имеют наименьшую дисперсию в классе всех линейных не­смещенных оценок (Best Linear Unbiased Estimator или BLUE).

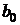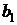Таким образом, оценки  и  яв­ляются наиболее эффективными линейными оценками парамет­ров регрессии.