Оценка качества и значимости модели множественной регрессии

Для оценки качества модели множественной регрессии используют следующие показатели:

· средняя ошибка аппроксимации – характеризует среднее отклонение расчетных значений  от фактических значений y. Величину  определяют по формуле (2.9);

· коэффициент множественной детерминации 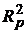– характеризует долю вариации результативного признака, обусловленную регрессией или изменчивостью факторов. Чем ближе  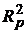к единице, тем лучше регрессия описывает зависимость между факторами и результативным признаком.

.

(3.18)

Вместе с тем использование только одного коэффициента детерминации 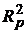 для выбора наилучшего уравнения регрессии может оказаться недостаточным. На практике встречаются слу­чаи, когда плохо определенная модель регрессии может дать сравнительно высокий коэффициент .

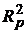Недостатком коэффициента детерминации 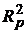 является то, что он увеличивается при добавлении новых факторов, хотя при этом качества регрессионной модели может не улучшиться. Предпочтительнее использовать скорректированный коэффициент детерминации , определяемый по формуле

.

(3.19)

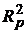Данная формула показывает, что чем больше число объясняющих пере­менных p, тем меньше   по сравнению с . Скорректированный коэффициент   может уменьшаться при введении в модель новых факторов, не оказы­вающих существенного влияния на результативный признак. Од­нако даже увеличение скорректированного коэффициента детер­минации  при введении в модель нового фактора не всегда означает, что ее коэффициенты регрессии зна­чимы. Это происходит только в случае, если соответствующее значение t -статистики больше единицы по аб­солютной величине, т. е. .

Если известен коэффициент детерминации 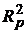, то критерий значимости уравнения регрессии имеет вид:

.

(3.20)

· t-критерий. Выдвигается гипо­теза 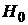 о случайной природе параметров уравнения регрессии , , , …, . Оценку значимости этих параметров выполняют с помощью t-критерия Стьюдента путем сопос­тавления их значений с величиной случайных ошибок:

.

(3.21)

Случайные ошибки параметров определяют по формулам:

	;	(3.22)
	;	(3.23)
	…
	,	(3.24)

где 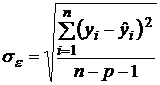; – обращенный определитель системы, в котором каждый элемент 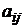 равен ; – алгебраическое дополнение элемента 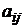, получаемое путем вычеркивания i -й строки и j -го столбца из определителя ; 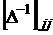– элемент обращенного определителя, стоящий на главной диагонали.

Сравнивая фактическое  и критическое (табличное)  значения t-статис­тик  с , принимают или отвергают гипотезу .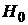

3.5. Прогнозирование значений результативного признака
с использованием модели множественной регрессии

При прогнозировании ожидаемого значения результативного фактора рассчитывают точечную и интервальную оценки.

Точечную оценку (прогнозное значение) 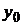 определяют путем подстановки в урав­нение регрессии (3.1) соответствующих прогнозных зна­чений факторов, которые следует записать в виде вектора-строки . Затем вычисляют среднюю стандартную ошибку прогноза. Для ожидаемого среднего значения  уравнение ошибки прогноза имеет вид:

,

(3.25)

где – вектор-столбец, содержащий те же элементы, что и вектор-строка .

Затем определяют интервальную оценку (доверительный интервал прогноза):

(3.26)

где .

Для ожидаемого индивидуального значения 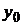 уравнение ошибки прогноза 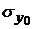имеет вид:

.

(3.27)

Затем определяют интервальную оценку (доверительный интервал прогноза):

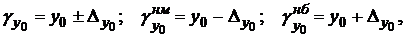
(3.28)

где .

ВРЕМЕННЫЕ РЯДЫ