Моделирование тенденции временного ряда

 

Построение аналитической функции для моделирования тенден­ции (тренда) временного ряда называют аналитическим выравнива­нием временного ряда. Для этого чаще всего применяют следую­щие функции:

· линейную ;

· гиперболу ;

· экспоненту ;

· степенную функцию ;

· параболу второго и более высоких порядков .

Параметры трендов определяют обычным МНК. В качестве не­зависимой переменной выступает время , а в качестве зависимой переменной – фактические уровни временного ряда . Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации .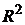

При построении моделей регрессии по временным рядам для устранения тенденции используют следующие методы.

Метод отклонений от тренда предполагает вычисление трендовых значений для каждого временного ряда модели, например  и , и расчет отклонений от трендов:  и . Для дальнейшего анализа используют не исходные данные, а отклонения от тренда.

Метод последовательных разностей заключается в следующем:

· если ряд содержит линейный тренд, то исходные данные заменя­ются первыми разностями:

;

(4.3)

· если ряд содержит параболический тренд – то вторыми разностями:

.

В случае экспоненциального и степенного тренда метод после­довательных разностей применяется к логарифмам исходных дан­ных.

Модель, включающая фактор времени, имеет вид

.

(4.4)

Параметры а и b этой модели определяются обычным МНК.

Автокорреляция в остатках – корреляционная зависимость между значениями остатков , за текущий и предыдущие моменты времени.

Для определения автокорреляции остатков используют критерий Дарвина–Уотсона и рассчитывают величину

, .

(4.5)

Коэффициент автокорреляции остатков первого порядка опреде­ляют по формуле

, .

(4.6)

Критерий Дарбина–Уотсона и коэффициент автокорреляции остатков первого порядка связаны соотношением

.

(4.7)

Эконометрические модели, содержащие не только текущие, но и лаговые значения факторных переменных, называются моделями с распределенным лагом.

Модель с распределенным лагом в предположении, что макси­мальная величина лага конечна, имеет вид

.

(4.8)

Коэффициент регрессии  при переменной  характеризует среднее абсолютное изменение  при изменении  на 1 единицу своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора х. Этот коэффициент назы­вают краткосрочным мультипликатором.

В момент  воздействие факторной переменной  на резуль­тат  составит  условных единиц; в момент времени  воздействие можно охарактеризовать суммой  и т. д. Эти суммы называют промежуточными мультипликаторами. Для мак­симального лага  воздействие фактора на результат описывают суммой , которую называют долгосрочным мультипликатором.

Величины

, где

(4.9)

называют относительными коэффициентами модели с распреде­ленным лагом. Если все коэффициенты 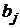 имеют одинаковые знаки, то для любого j

, и

(4.10)

Величину среднего лага модели множественной регрессии опре­деляют по формуле средней арифметической взвешенной:

(4.11)

и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент t.

Медианный лаг – это период, в течение которого с момента вре­мени t будет реализована половина общего воздействия фактора на результат:

,

(4.12)

где – медианный лаг.

Оценку параметров моделей с распределенными лагами можно проводить согласно одному из двух методов: методу Койка или ме­тоду Алмон.

В методе Койка предполагается, что коэффици­енты при лаговых значениях объясняющей переменной убывают в геометрической прогрессии:

, , .

(4.13)

Уравнение регрессии преобразуют к виду

.

(4.14)

После несложных преобразований получаем уравнение, оценки параметров которого приводят к оценкам параметров исходного уравнения.

В методе Алмон предполагается, что веса текущих и лаговых значений объясняющих переменных подчиняются полиномиальному распределению:

.

(4.15)

Уравнение регрессии примет вид

,

(4.16)

где , ,

Расчет параметров модели с распределенным лагом методом Алмон проводят по следующей схеме:

1) устанавливают максимальную величину лага l;

2) определяют степень полинома k, описывающего структуру лага;

3) рассчитывают значения переменных ;

4) определяют параметры уравнения линейной регрессии  от ;

5) рассчитывают параметры исходной модели с распределенным лагом.

Модели, содержащие в качестве факторов лаговые значения зави­симой переменной, называют моделями авторегрессии, например:

.

(4.17)

Как и в модели с распределенным лагом,  в этой модели харак­теризует краткосрочное изменение  под воздействием изменения  на 1 единицу. Долгосрочный мультипликатор в модели авторегрессии рас­считывают как сумму краткосрочного и промежуточных мульти­пликаторов:

.

(4.18)

Отметим, что такая интерпретация коэффициентов модели авто­регрессии и расчет долгосрочного мультипликатора основаны на предпосылке о наличии бесконечного лага в воздействии текущего значения зависимой переменной на ее будущие значения.