2018-02-13
224
Для оценки тесноты связи между последовательностями наблюдений временного ряда 
и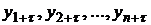 
, сдвинутых друг относительно друга на 
единиц (с лагом ) используют понятие автокорреляции.
Автокорреляция уровней ряда – это корреляционная зависимость между последовательными уровнями временного ряда.
Коэффициент автокорреляции 
первого уровня ряда между соседними уровнями рядов 
и 
, т. е. при лаге 1 определяют по формуле
 ,
| (4.1) |
где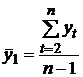 
; 
.
Коэффициент автокорреляции 
второго уровня ряда между соседними уровнями рядов и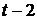 
, т. е. при лаге 2 определяют по формуле
 ,
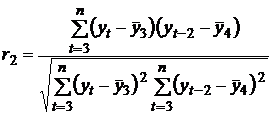| (4.2) |
где 
; 
.
Например, если известны данные о средних расходах на конечное потребление за 8 лет, то временной ряд с лагами 1 и 2 можно представить в виде таблицы (табл. 4.1)
Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют автокорреляционной функцией временного ряда, а график зависимости ее значений от величины лага (порядка коэффициента автокорреляции) – коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а следовательно, и лаг, при котором связь между текущим и предыдущими уровнями ряда наиболее тесная, т, е. при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка , ряд содержит циклические колебания с периодичностью в моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний и имеет структуру, сходную со структурой ряда, изображенного на рис. 5.1 в), либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно проверти дополнительный анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты (Т) и циклической (сезонной) компоненты (S).
