2018-02-13
204
ЗНАХОДЖЕННЯ ОЦІНОК МЕТОДОМ НАЙМЕНШИХ КВАДРАТІВ З ЗАСТОСУВАННЯМ МАТРИЧНОЇ ФОРМИ ЗАПИСУ
Задана вибірка трьох змінних 
, 
, 
, які входять в економетричну модель, у вигляді таблиці
|
| 4 | 5 | 6 | 8 | 11 | 11 | 12 | 12 | 13 | 14 |
|
| 3 | 4 | 5 | 7 | 9 | 11 | 10 | 12 | 11 | 12 |
|
| 7 | 9 | 11 | 12 | 12 | 15 | 18 | 21 | 22 | 24 |
Знайти вектор оцінок 
і матрицю дисперсій оцінок 
.
Розв’язування.
Допустимо, що між показником і факторами , існує лінійна залежність
Знайдемо оцінки параметрів, використовуючи матричні операції за формулою
, де
-матриця пояснюючих змінних X 1, X 2 , доповнена колонкою одиниць, 
- вектор результативної змінної Y, 
- транспонована матриця пояснюючих змінних.
Проведемо відповідно обчислення
.
= 
.
Наступним кроком є обчислення добутку матриці і вектора 
:
= 
ґ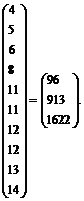 
Тоді вектор оцінок
ґ 
= 
.
Отже економетрична модель має вигляд:
.
Знаходимо матрицю дисперсій оцінок:
,
де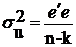 
, 
- вектор відхилень значень змінної Y і із вибірки від розрахункових значень цієї змінної 
,
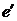- транспонований вектор , n – об’єм вибірки, k – кількість змінних, які входять в модель.
Діагональні елементи матриці визначають дисперсії оцінок 
, 
, 
. Інші елементи взаємну коваріацію цих оцінок. З допомогою діагональних елементів матриці 
знаходяться граничні похибки оцінок для заданого рівня ймовірності.
Знаходимо розрахункові значення
; 
і т. д. 
.
Обчислюємо вектор відхилень:
=4 -4,12 = -0,12;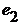 
= 5 - 5,19 = -0,19; і т. д. 
= 14 - 13,65 = 0,35.
= 
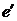
= 4,82.
= 4,82/(10-3) = 0,69.
= 0,69 ґ 
= 
.
