2018-02-14
363
Уравнения движения вязкой жидкости (2.38) имеют ограниченное число точных решений, в частности, в случае так называемых слоистых течений. Рассмотрим примеры.
А) Течение в плоском канале. Рассмотрим стационарное течение между двумя покоящимися параллельными плоскими стенками. Направим ось O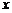 
по оси канала, ось O 
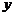– перпендикулярно. Тогда естественно положить, что 
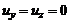. Уравнение для продольной составляющий скорости 
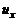примет вид
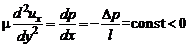, (2.39)
где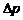 
– заданный перепад давления на участке канала длиной 
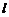. Если расстояние между стенками 
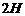, то граничные условия таковы: 
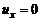при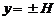 
.
Дважды проинтегрировав уравнение (2.39), получим параболический профиль скорости
,
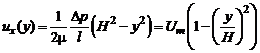где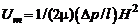 
– максимальное значение скорости, достигаемое на оси канала. Объемный расход [по (2.10), где 
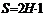м]
;
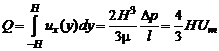средняя скорость согласно (2.12)
.
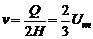Напряжение трения на стенке
.
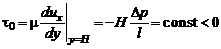Зная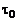 
, можно определить силу сопротивления трения участка канала, приходящуюся на 1 м в направлении координаты 
:
.
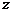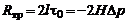б) Течение в круглой трубе (течение Хагена–Пуазейля). Введем цилиндрические координаты (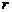
, 
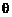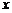, ), причем пусть ось трубы совпадает с осью O 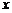. Предположим, что поле скорости 
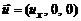осесимметрично, т.е. продольная компонента скорости 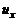зависит только от радиальной координаты 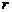. Уравнение движения принимает вид
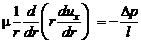(2.40)
с граничным условием: 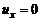при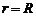 
. Проинтегрировав (2.40), получим
• профиль скорости
,
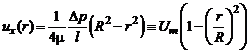где максимальная скорость (скорость на оси трубы)
;
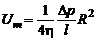• объемный расход
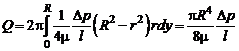(2.41)
(закон Хагена–Пуазейля);
• среднюю скорость
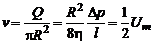; (2.42)
• напряжение на стенке
;
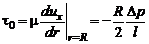• силу сопротивления трения участка трубы
.
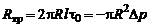Интеграл Бернулли для потока весомой
несжимаемой вязкой жидкости
Займемся обобщением интеграла Бернулли на случай движения тяжелой вязкой жидкости.
Исходим из того, что движение установившееся и в рассматриваемом сечении поток слабо деформирован. (Под слабодеформированными понимают потоки, у которых угол расхождения линий тока мал, а радиус кривизны – велик.)
Определим энергию, проносимую секундной массой струйки через сечение (т.е. мощность струйки). Эта величина может быть найдена как произведение полной удельной энергии струйки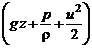 
на ее массовый расход (
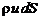). Таким образом,
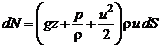. (2.43)
Секундная энергия (мощность) потока в соответствии со струйной моделью
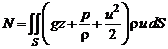(2.44)
либо
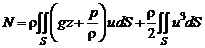. (2.45)
Так как поток слабодеформированный, то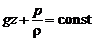 
и после преобразований получаем
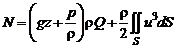. (2.46)
По физическому смыслу второй член в (2.46) представляет собой кинетическую энергию секундной массы. Отсюда, разделив обе части уравнения на массовый расход потока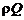 
, получим удельную энергию
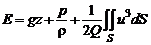
или
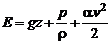, (2.47)
где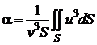 
– коэффициент Кориолиса, представляющий собой отношение кинетической энергии потока, вычисленной по истинному распределению скоростей, к кинетической энергии, вычисленной по средней скорости.
Разделив обе части (2.47) на ускорение свободного падения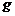 
, выразим это соотношение в единицах длины, т.е. в форме напоров
.
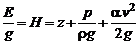Рассмотрим движение потока вязкой жидкости в канале (рис. 2.8) от сечения 1-1 к сечению 2-2. Обозначим удельную энергию потока в сечении 1-1 через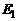 
, а в 2-2 – 
.
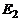Так как жидкость вязкая, то процесс ее перемещения сопровождается диссипацией энергии, т.е. какая-то ее часть расходуется на преодоление сил внутреннего трения и превращается в тепло, следовательно,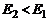 
. Поэтому баланс энергии для выбранных сечений должен быть записан в виде
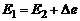, (2.48)
где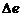 
– потери энергии.
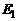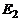Раскрывая значения и , получаем:
. (2.49)
Это и есть энергетическая форма интеграла Бернулли для потока вязкой жидкости.
В практических приложениях чаще используют интеграл Бернулли, выраженный в напорах
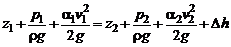, (2.50)
где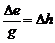 
– потери напора.
Для газовых потоков (без учета сжимаемости), а также при расчетах систем гидравлического привода обычно используют уравнение Бернулли в форме давлений
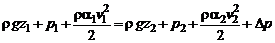, (2.51)
где 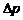– потери давления. Как правило, в упомянутых системах член 
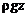оказывается пренебрежимо малым по сравнению с остальными.
В этих случаях (2.51) принимает вид
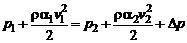. (2.52)
Основы гидравлики
Предметом изучения в гидравлике служат законы движения жидкостей в открытых и закрытых каналах, гидротехнических сооружениях и гидромашинах, имеющие направленность на решение широкого круга вопросов инженерной практики. Теоретической основой гидравлических расчетов служит обобщенный интеграл Бернулли в форме (2.49) – (2.52).
3.1. Гидравлические потери
На распределенных и местных
сопротивлениях
