Режимы течения жидкости в трубах. Опыты Рейнольдса

 

Историографы гидроародинамики называют XIX век "золотым" не только благодаря выдающимся результатам в исследовании и создании летательных аппаратов тяжелее воздуха, но и разгадкой одной из самых удивительных и сложных гидродинамических загадок XIX века. 1880 год можно назвать годом, когда странное противоречие, постепенно раздирающее гидравлику, достигло кульминации. И, что самое оригинальное, вызвано оно было не вследствие отсутствия надежных сведений, а наоборот, большим объемом достоверных и тщательных экспериментов, неопровержимо доказывающих справедливость двух совершенно противоположных утверждений. Начало этому положил немецкий инженер-строитель Г.Гаген. В 1839 году он опубликовал результаты своих обширных исследований по изучению влияния температуры на сопротивление жидкости, текущей в трубках малого диаметра (капиллярах), и вывел формулу для вычисления сопротивлений.

Одновременно с ним подобные эксперименты провел французский врач Ж.Пуазейль, который изучал работу сердца и движение крови в венах и капиллярных сосудах. Им получена формула, совпадающая с формулой Г.Гагена в виде

.                                    (6.12)

Очевидно, что левая часть этого выражения есть ничто иное, как удельная (отнесенная к массе жидкости m) сила сопротивления R. Воис­тину, формула эта доставляет утешение здравому смыслу, чем больше вязкость ν и меньше диаметр трубы d, тем труднее двигаться жидкости. Ясно, что чем больше скорость движения V, тем больше сила сопротив­ления.

Однако, коварная гидравлика приберегла свой сюрприз напоследок. Бельгийский инженер А.Дарси, прославившийся как строитель водопровода у себя на родине в Дижоне и затем в Брюсселе, получил по исследованиям течения воды в трубах, проведенным в ходе строительства водопроводов, совсем иную формулу. Сопротивление в опытах Дарси получилось прямо пропорционально квадрату скорости и обратно пропорционально диаметру трубы:

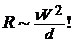
Весь трагизм ситуации заключался в следующем. С одной стороны, англичанин Дж. Стокc, швейцарец Э. Гагенбах, немец Ф. Нейман, будучи добросовестнейшими экспериментаторами, опыт за опытом получали подтверждение правоты Пуазейля. С другой стороны, не менее добросовестные исследователи англичанин Дж. Ранкин, немец О. Майер и др. получали результаты, говорящие, что прав Дарси. Особенно тяжело было Гагену, который проверяя свои и Пуазейля опыты убеждался в своей правоте, а экспериментируя с водопроводными трубами, получал подтверждение результатов Дарси.

Решение проблемы было найдено благодаря усилиям и таланту ученых-инженеров - русскому Н.П. Петрову и английскому О. Рейнольдсу.

Н.П. Петров известен своей разработкой гидродинамической теории смазки. В ней он ясно указал на существование двух различных режимов течения жидкости в трубе. Первый режим им представлялся как прямолинейное движение жидкости в виде вложенных один в другой цилиндрических слоев параллельно оси трубы. Сопротивление в этом случае пропорционально первой степени скорости.

При втором режиме в движущейся жидкости образуются вихри, разрывы струек и поперечные движения частиц. Сопротивление движению становится пропорционально квадрату скорости. Эти наблюдения Петрова стали ключевой идеей в замечательных открытиях английского гидродинамика О. Рейнольдса.

Особенности режимов движения жидкости можно наглядно наблюдать на установке, схема которой приведена на рис.6.3.

 

 

Рис. 6.3. Схема экспериментальной установки Рейнольдса

 

К достаточно большому по объему баку 3 присоединена стеклянная труба 5, в конце которой установлен вентиль 6. Этим вентилем можно менять расход жидкости в трубе, который измеряется при помощи мерного бака 7. Над баком 3 расположен сосуд 1 с раствором краски, плот­ность которого близка к плотности исследуемой жидкости. Краска вво­дится в поток при помощи трубки 4. Количество подаваемой краски ре­гулируется вентилем 2. В процессе проведения экспериментов уровень жидкости в баке 3 поддерживается постоянным.

При определенном открытии вентиля б в трубе 5 установится неко­торая скорость потока и при открытии крана 2 в поток поступит струйка краски.

При малой скорости потока жидкости в трубе 5 краска образует прямолинейную и резко выделяющуюся не смешивающуюся с окружающей жидкостью струйку. Заметного обмена частицами между струйкой краски и окружающей ее жидкостью не происходит. При этом никакого значения не имеет, в каком месте поперечного сечения трубы была выпущена струйка краски. Это свидетельствует о том, что при данном открытии вентиля 6 жидкость движется отдельными не перемешивающимися слоями. Измерения давления и скорости показывают их неизменность во времени, т.е. отсутствуют пульсации. Такой режим движения называется ламинарным.

Ламинарное движение является вполне упорядоченным и при постоянном напоре установившимся течением (хотя в общем случае может быть и неустановившимся). Однако, его нельзя считать безвихревым, т.к. в нем хотя и нет видимых вихрей, но одновременно с поступательным движением имеет место упорядоченное вращательное движение отдельных частиц жидкости вокруг своих мгновенных центров с некоторыми угловыми скоростями.

При постепенном открытии вентиля 6 скорость потока жидкости в трубе будет увеличиваться. Вначале это не приведет к изменению кар­тины течения жидкости, но затем при определенной скорости течения наступает быстрое ее изменение. Струйка краски при выходе из трубки 4 начинает двигаться волнообразно, затем разрываться и перемешивать­ся с потоком жидкости. При этом становятся заметными вихреобразования и вращательное движение жидкости. Измерения показывают непрерывные пульсации давления и скорости в потоке жидкости. Такой режим течения принято называть турбулентным.

При турбулентном течении векторы скоростей имеют не только продольные (осевые), но и поперечные составляющие. Поэтому наряду с основным осевым перемещением жидкости вдоль трубы происходят поперечные неупорядоченные перемещения как жидких частиц, так и отдельных объемов жидкости.

На рис.6.4. приведена примерная картина изменения характера течения потока жидкости при изменении его скорости.

 

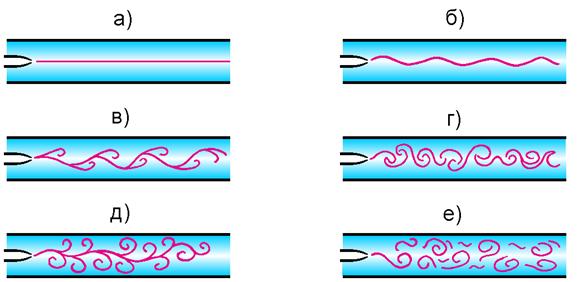
Рис.6.4. Изменение картины течения жидкости в трубе

с увеличением скорости течения от а к е

 

На основе многочисленных и многолетних (более 10 лет) экспери­ментов Рейнольдс установил, что существуют некоторые критические скорости, при которых происходит смена режимов течения жидкости. Рейнольдс обнаружил существование двух критических скоростей.

Одна имеет место при переходе ламинарного режима движения в турбулентный режим, она называется верхней критической скоростью V_KP.B, другая -при переходе турбулентного режима движения в ламинарный режим, она называется нижней критической скоростью V_KP.Н.

Задержка (V_KP.Н <V_KP.B) с обратным переходом, очевидно, обусловлена необходимостью успокоения течения жидкости. Опытным путем доказано, что значение верхней критической скорости меняется довольно в широких пределах в зависимости от внешних условий: постоянства температуры, уровня вибрации экспериментальной установки и т.п. В противоположность ей нижняя критическая скорость в широком диапазоне изменения внешних условий остается практически постоянной. Как показывают опыты, значение этой скорости прямо пропорционально кинематической вязкости ν и обратно пропорционально диаметру трубы d:

.

Входящий в эту формулу безразмерный коэффициент пропорциональности k одинаков для всех жидкостей и газов, а также для любых диаметров труб. Это означает, что изменение режима течения происходит при определенном соотношении между скоростью, диаметром и кинематической вязкостью.

Полученное безразмерное число называется критическим числом Рейнольдса и обозначается

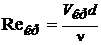.                                (6.13)

Этот результат согласуется с формулой критерия подобия (6.5) и вполне закономерно, что именно число Рейнольдса является критерием, определяющим режим течения в трубах.

Рейнольдс установил, что для труб круглого сечения Re_кp = 2320.

Таким образом, число Рейнольдса позволяет судить о режиме тече­ния жидкости в трубе. При Re < Re_кp будет ламинарный режим, а при
Re > Re_кp - турбулентный.

Строго говоря, такого резкого перехода действительно нет. Смена режима течения при достижении Re_кp обусловлена тем, что одно течение теряет устойчивость, а другое - приобретает. При Re < Re_KP ламинарный режим течения вполне устойчив. Всякого рода искусственная турбулизация потока погашается влиянием вязкости, и ламинарное течение восстанавливается.

При Re > Re_кp наоборот, турбулентное течение устойчиво, а ламинарное - неустойчиво. Однако, в особых лабораторных условиях при полном отсутствии факторов, способствующих турбулизации потока, получают ламинарный режим и при Re = (3-5)×10⁴. Таким образом, при Re = 2320 - 40000 имеет место переходная, область.

На практике обычно имеются условия, способствующие турбулизации, - вибрации труб, местные гидравлические сопротивления, неравномерность (пульсация) расхода и др., а потому указанное обсто­ятельство имеет скорее принципиальное, чем практическое значение. В природе и технике турбулентное движение жидкости наблюдается чаще, чем ламинарное.

 

ЛАМИНАРНОЕ ТЕЧЕНИЕ

 

Как отмечалось выше, ламинарное течение характеризуется парал­лельно-струйчатым упорядоченным движением частиц жидкости. Движение можно представить как совокупность бесконечно тонких кольцевых концентрических слоев, перемещающихся относительно друг друга. Единственным источником потерь энергии в данном случае является трение между слоями движущейся жидкости, подчиняющееся закону трения Ньютона.

Рассмотрим установившееся ламинарное течение жидкости в прямой круглой трубе с внутренним диаметром d = 2r. Расположим трубу горизонтально. Этим мы исключим влияние силы тяжести и упростим вывод. Достаточно далеко от входа в трубу, где поток стабилизировался, выделим участок длиной 1 двумя сечениями 1-1 и 2-2 (рис.6.5).

 

 

Рис.6.5. Схема к теории ламинарного течения жидкости в трубе

 

Запишем уравнение Бернулли для выделенного участка. Согласно (5.16) имеем

.          (6.14)

Вследствие неизменности диаметра трубы и стабильности потока V₁ =V₂ и L₁ = L₂. Так как труба горизонтальная, то z₁ = z₂. Отсюда выра­жение (6.14) примет вид

.

Тогда потери на трение по длине составят

.                          (6.15)

Выделим цилиндрический объем радиусом r, соосный с трубой и имеющий основания в выбранных сечениях. Составим уравнение равномерного движения этого объема, т.е. равенство нулю суммы сил, действующих на объем. Такими силами являются силы давления и вязкости. Обозначая через t касательные напряжения на боковой поверхности цилиндра, получим

.

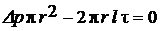Из этой формулы касательные напряжения определяются как

,                                       (6.16)

т.е. они изменяются по линейному закону в функции радиуса.

Эпюра касательных напряжений приведена на рис.6.5. Отметим, что эта эпюра не зависит от режима течения жидкости.

В свою очередь, согласно формуле (1.18) касательные напряжения для рассматриваемого случая описываются выражением

.                                    (6.17)

В этом выражении переменная у (расстояние от стенки) заменена текущим радиусом r. Знак минус обусловлен тем, что направление отс­чета у (от стенки) противоположно направлению отсчета r (от оси).

Приравнивая выражения (6.16) и (6.17), получим .

Отсюда приращение скорости составит .

Проинтегрировав это выражение, будем иметь .

Постоянная интегрирования находится из граничных условий.

При r = r_о имеем V = 0 и .

Тогда формула скорости по окружности радиусом r имеет вид

.                                    (6.18)

Это выражение является законом распределения скоростей по живому сечению круглой трубы при ламинарном режиме течения. Кривая, изображающая эпюру скоростей, представляет собой квадратичную параболу (рис.6.5).

Максимальная скорость частиц жидкости будет на оси трубы
(г = 0)

.                              (6.19)

Расход через элементарную площадку dS составит dQ = VdS, или согласно (6.18) и dS = 2πrdr будет

Проинтегрировав это выражение от r = 0 до r = r_о, т.е. по всей площади живого сечения, получим

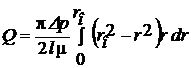 и .          (6.20)

Средняя скорость по живому сечению составит

.                              (6.21)

Сравнивая между собой формулы (6.19) и (6.21), получим

Зная закон распределения скоростей по сечению потока, можно оп­ределить величину коэффициента кинетической энергии – коэффициента Кориолиса.

Подставим в формуле (5.14) среднюю скорость по выражению (6.21) и V_i по формуле (6.18).

Тогда

Имея в виду, что  и , получим

Таким образом, действительная кинетическая энергия потока при ламинарном режиме течения в два раза превышает кинетическую энергию того же потока, но при равномерном распределении скоростей.

Определим зависимость потерь напора h_1-2 на трение от параметров потока.

Для этого из выражения (6.20) определим перепад давления Dр:

.

Имея в виду, что µ= νr и r_о = d/2, а также согласно. (6.15) получим

                         (6.22)

Эта формула получена Пуазейлем и носит его имя. С ней полностью согласуется формула (6.12), представляя ее другой вид.

Формула (6.22) широко используется для расчета трубопроводов с ламинарным режимом течения.

В 5.4 потери по длине трубы представлены в виде зависимости от средней скорости по формуле Вейсбаха-Дарси (5.22).

Для приведения формулы (6.22) к подобному виду заменим в ней расход Q его выражением через среднюю скорость

Тогда

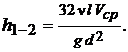                            (6.23)

Из этого выражения видно, что при ламинарном режиме течения жидкости потери действительно пропорциональны скорости в первой степени, как утверждали Гаген и Пуазейль.

Для окончательного приведения формулы потерь на трение по длине (6.23) к виду формулы Вейсбаха-Дарси (5.22) приравниваем их

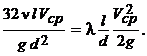
Отсюда коэффициент Дарси для ламинарного потока (_л) будет

или имея в виду , получим 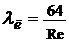, и окончательно

                         (6.24)

Как уже отмечалось, при установившемся ламинарном движении линии тока и траектории жидких частиц совпадают и это - прямые, параллельные направлению движения.

Если направить ось ОХ ортогональной системы координат XYZ вдоль оси трубы, то проекции скорости частицы жидкости согласно (6.18) будет

где

Видно, что единственная, не равная нулю проекция скорости не за­висит от координаты X. Компоненты угловой скорости по (3.13) составят

     (6.25)

Дифференциальное уравнение вихревой линии (3.16)

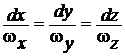
после подстановки в него (6.25) примет вид  и после интегрирования получим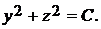

Таким образом, вихревые линии в данном случае представляют собой концентрические окружности с центрами на оси трубы.

Угловая скорость частиц жидкости по (3.14) составит

,

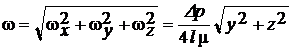Или .                                      (6.26)