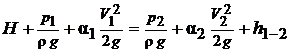В данном случае имеем

.

Потери удельной энергии на участке определяются сопротивлением отверстия (местные потери) и представим их в виде формулы Вейсбаха

,

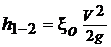где ξ₀ - коэффициент потерь при истечении из отверстия с острой кромкой.

Перенесем известные члены уравнения в его левую часть

.

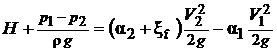Учитывая, что уравнение неразрывности V₂S₂ = V₁S₁ или V₂DS_o = V₁S₁ (S₁ и S₂ - площади свободной поверхности жидкости в резервуаре), можем записать

.

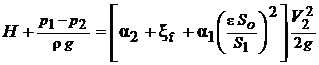Отсюда в общем случае (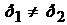) средняя скорость в сжатом се­чении определится как

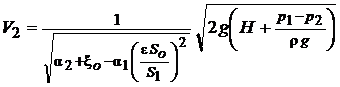             (7.2)

Множитель 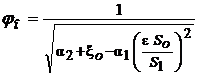 называется коэффициентом скорости.

Тогда 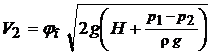           .            (7.3)

На практике часто встречается ситуация, когда р₁ = р₂ = р_атм т.е. имеем открытый резервуар и истечение струи происходит в окру­жающую атмосферу.

Тогда формула (7.3) примет вид 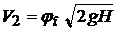          .       (7.4)

Расход жидкости через отверстие составит 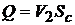  или с учетом (7.1) .

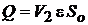Используя (7.3) получим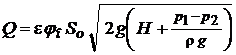               

или в случае использования (7.4) будет .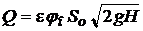

Произведение коэффициентов µ_o = ε φ_о называют коэффициентом расхода. Тогда

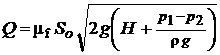.                       (7.5)

или 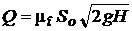                                      .                            (7.6)

Как уже отмечалось выше, распределение скоростей по сечению струи является равномерным лишь в средней части сечения (в ядре струи). Опыт показывает, что в ядре струи скорость практически равна идеальной

.

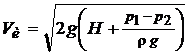Поэтому введенный коэффициент скорости  следует рассматривать как коэффициент средней скорости.