2018-02-14
598
Резерфорд предложил ядерную модель атома: вокруг положительно заряженного ядра, имеющего заряд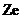 
(
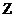– порядковый номер элемента), по замкнутым орбитам движутся электроны, образуя электронную оболочку атома. Кулоновская сила взаимодействия сообщает электрону центростремительное ускорение. Второй закон Ньютона для электрона, движущегося по окружности: 
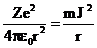, где 
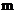и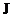 
– масса и скорость электрона на орбите радиуса 
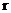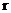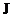. Недостаток уравнения в том, что оно содержит два неизвестных и . Следовательно, существует бесчисленное множество значений радиусов и скоростей, а значит и энергий, которая может меняться непрерывно, и следовательно, испускаться любая порция энергии. Этому противоречит линейчатый спектр излучения атомов. Попытки построить теорию атома в рамках классической физики не привели к успеху. Первая попытка построить новую квантовую теорию атома была предложена Бором. В основу теории Бор положил два постулата:
I постулат (постулат стационарных состояний). В атоме существуют стационарные (не изменяющиеся во времени) состояния, в которых он не излучает энергии. Стационарным состояниям соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по ним не сопровождается излучением электромагнитных волн. В стационарном состоянии атома электрон должен иметь дискретные квантовые значения момента импульса, удовлетворяющие условию: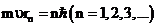 
.
II постулат (правило частот). При переходе электрона с одной стационарной орбиты на другую излучается или поглощается один фотон с энергией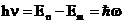 
, равной разности энергий соответствующих стационарных состояний. 
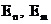– энергии электрона на соответствующих орбитах. Решая совместно уравнение Резерфорда с условием первого постулата Бора, найдем радиус стационарной орбиты электрона 
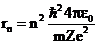, тогда энергия электрона на 
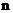-ой стационарной орбите: 
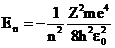. Полученные энергетические состояния атома образуют последовательность энергетических уровней, изменяющихся в зависимости от значения 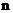, где 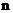– главное квантовое число. Состояние атома для значения главного квантового числа 
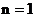называется основным или нормальным состоянием; если 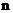> 1 – состояния называются возбужденными.
В квантовой механике состояние электрона в атоме водорода (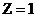
) описывается волновой функцией 
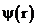, удовлетворяющей стационарному уравнению Шредингера:
.
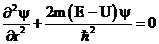Потенциальная энергия взаимодействия электрона с ядром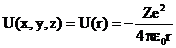 
, тогда 
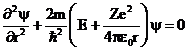. Решение этого уравнения позволяет найти собственные значения энергии электрона:
.
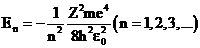Энергия принимает дискретные отрицательные значения. Выражение для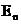 
совпадает с формулой, полученной Бором для энергии электрона в атоме водорода, однако, если Бору пришлось вводить дополнительные гипотезы (постулаты), то в квантовой механике дискретные значения энергии вытекают непосредственно из решения уравнения Шредингера.
Квантовые числа
Квантовые числа – это целые или полу целые числа, определяющие возможные дискретные значения физических величин системы, подчиняющиеся квантовым законам.
Главное квантовое число 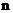, определяет энергетические уровни электрона в атоме, 
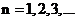Электроны со значениями энергии, соответствующими главному квантовому числу 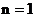образуют К-оболочку; со значениями 
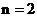– L-оболочку, 
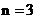– М-оболочку, и т.д.
Из решения уравнения Шредингера вытекает, что механический орбитальный момент импульса электрона квантуется, принимая дискретные значения, определяемые формулой 
, где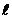 
– орбитальное квантовое число. Оно определяет форму орбиты и принимает значения 
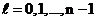, т.е. всего 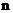значений. Например, при 
, 
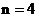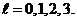Если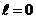 
– это s-электрон, при 
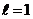– р-электрон, при 
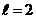– d-электрон, и т.д.
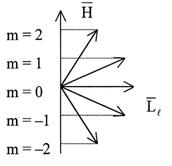Из решения уравнения Шредингера следует, что вектор 
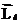орбитального момента импульса электрона может быть только так ориентирован в пространстве, когда его проекция 
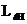на направление внешнего магнитного поля принимает только квантованные значения 
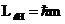, где 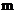– магнитное квантовое число. Оно определяет проекцию 
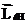на направление внешнего магнитного поля 
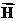и характеризует ориентацию плоскости электронной орбиты в пространстве, принимая значения 
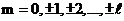, всего 
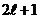значений ориентаций.
Хотя энергия электрона и зависит только от квантового числа 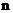, но каждому собственному значению энергии 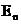соответствует несколько собственных функций 
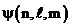, отличающихся значениями 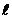и 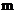. Значит, атом водорода может иметь одно и то же значение энергии, находясь в различных состояниях. Число различных состояний, соответствующих главному квантовому числу 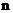, равно 
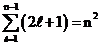. Состояния с одинаковым значением энергии называются вырожденными, а число таких состояний с одинаковыми значениями энергии называется кратностью вырождения соответствующего уровня. Каждый уровень энергии водородоподобного атома имеет кратность вырождения, равную 
.
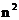Спин электрона
Кроме орбитальных магнитного (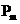
) и механического (
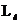) моментов электрона, определяющих его движение по орбите, электрон обладает собственным механическим моментом импульса. Он носит название спина - 
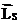и не связан с движением электрона в пространстве. Следствием наличия спина является существование собственный магнитный момент 
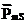. Эти моменты являются внутренними неотъемлемыми свойствами электрона, такими же, как заряд и масса. Спин может принимать лишь дискретные значения и квантуется по закону 
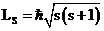, где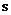 
– спиновое квантовое число. Для электрона, протона и нейрона 
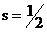, для фотона 
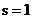. Проекция спина 
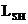на направление внешнего магнитного поля квантуется так, что вектор 
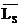может принимать только 
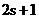ориентаций. Значит, для электрона (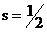) всего две ориентации.
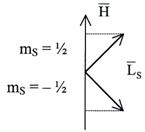
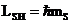, где 
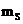– магнитное спиновое квантовое число. Для электрона оно принимает лишь два значения 
.
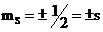Все элементарные частицы делятся на два класса.. Частицы с полу целым спином , (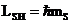
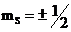; электроны, протоны, нейроны) называются фермионами. Частицы с целым спином (
; 
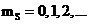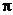-мезоны, фотоны, фононы) называются бозонами.
Принцип Паули
Распределение электронов по энергетическим уровням в атоме подчиняется принципу Паули: в атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел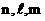 
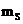и т.е.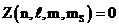 
или 1. Поскольку для электрона число 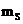принимает лишь два значения 
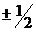, то на любом энергетическом уровне может находиться не более двух электронов с разными спинами. Максимальное число электронов, находящихся в состояниях, определяемых главным квантовым числом 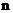равно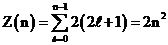 
, т.е. 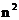-электронов с 
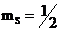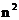и -электронов с 
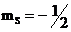. Отметим, что принципу Паули подчиняется распределение по энергетическим состояниям не только электронов, но и всех фермионов. Распределение бозонов принципу Паули не подчиняется.
