2018-02-14
219
Система приводится к стандартному виду:
x = E+Asinwt
E – смещение
Явление смещения возникает когда:
1) Присутствует несимметричная относительно (0,0) нелинейность
2) Есть постоянное возмущение
Ограничения по применению метода:
1) Передаточная функция линейной части не содержит полюсов в правой полуплоскости (это значит, что линейная часть устойчива)
2) Нет интеграторов
Если постоянная составляющая присутствует и никакого баланса быть не может если у нас неустойчивое звено, поэтому эта составляющая не будет постоянной, а будет зависеть от времени. Поэтому, если бы был хоть один интегратор, то он интегрируя эту составляющую, менял бы выход и баланс был бы недопустим.
Сигнал на выходе: 
, где 
- постоянная составляющая
Из метода гармонической линеаризации известно, что коэффициенты 
зависят от амплитуды, в нашем случае они зависят от двух переменных: амплитуды и смещения.
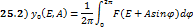
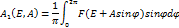
Введя эти коэффициенты мы линеаризовали нашу систему, поэтому справедливо считать, что периодическое решение является суммой двух решений: решения по постоянной составляющей и решения по первой гармонике.
Условие гармонического баланса можно записать так:
(Условие существования смещенного периодического решения)
Видно, что появляется три переменные: амплитуда, частота, смещение. Как отыскать решение?
Перепишем первое уравнение в виде:
А задаем как параметр:
Получим пары
решений:
25.3) Теперь воспользуемся вторым уравнением (Гольдфарба):
Строим годографы:
Годограф строится по тем точкам, которые мы нашли как решения. Затем проводим уточнение. Видим, что нужное пересечение находится между параметрами 
, поэтому возвращаемся в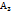 
и добавляем до нужного результата 
Вдоль кривой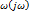 
нашли частоту 
а вдоль кривой J(E,A) значения E, 
