2018-02-14
224
Рассм-им покоящуюся, однородную, несжимаемую жидкость. С пространством, к-я она занимает свяжем прямоуг-ю систему координат. Рис.
В покоящейся ж выделим твердую частицу. Уравнения равновесия ж м. б получены из условия равновесия сил, действующих на элементар-ый параллелепипед, т.е на жидкую частицу. Чтобы не загромождать вывод рассмотрим равновесие сил в проекции на ось х. Полученные рез-ты м.б распространены на оставшиеся пространственные координаты. Левая и правая грань параллелипипеда отстоят от т. А на оис х ± 
. Выразим давление в центрах этих граней через давление вт. А: рл=р - 
,: рп=р+ 
, где 
= 
p(x,y,z) – частная производная, характериз-ая интенсивность изменения давления вдоль оси х, при неизменных значениях y,z, соответствующих центрам рассматриваемых граней. ± 
- приращения давления в центрах левой и правой граней относ-но давления в т. А. Принимая давления Рл и Рп в качестве средних на гранях можно определить элементарные силы давления на левую и правую грани. Силы, действующие на левую и правую грани параллелепипеда равны.
dFхл=рл*dS= (р - )dydz; dFхп=рп*dS= (р + )dydz; (1)
Кроме поверхностых сил dFхл и dFхп на параллелепипед действует массовые силы, равнодействующая к-х приложена в т. А и равна dM=ρdVj, ρ-плотность, dV- объем параллелепипеда = dxdydz, j- единичная массовая сила, j={jx=X, jy=Y, jz=Z}. Тогда проекция элементарной массовой силы будет равна:
dMx=ρXdxdydz (2), dFхл-dFхп+dMx=0, (1), (2)—послед-е уравнение:
(р- )dydz -(р + )dydz+ρXdxdydz=0. Если раскрыть скобки и привести подобные, а затем разделить каждое слагаемое на dxdydz, то получим: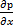 
=ρХ.
Рассуждая подобным образом можно придти к анологичным ур-ям для оставшихся пространственных координат и окнчательно записать:
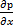=ρХ (3), 
=ρY (4), 
=ρZ (5). Уравнения (3), (4), (5) – это есть ДУ равновесия ж. Они были получены Леонардом Эйлером в 1755 и носят его имя. Из ураненеия Эйлера следует, что изменение гидростатического р вдоль координат x,y,z происходит за счет соответствующх проекций единичной массовой силы x,y,z.
