Линейная модель парной регрессии есть: у=а0+а1х+e
а1 - коэф-т регрессии, показывающий, как изменится у при изменении х на единицу
а0 - это свободный член, расчетная величина, содержания нет.
e - это остаточная компонента, т.е. случайная величина, независимая, нормально распределенная, мат ожид = 0 и постоянной дисперсией.
В матричной форме модель имеет вид:
Y=XA+ε
Где Y– вектор-столбец размерности (nx1) наблюдаемых значений зависимой переменной; Х– матрица размерности (nx2) наблюдаемых значений факторных признаков. Дополнительный фактор х0 вводится для вычисления свободного члена; А– вектор-столбец размерности (2х1) неизвестных, подлежащих оценке коэффициентов регрессии; ε– вектор-столбец размерности (nх1) ошибок наблюдений
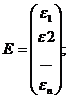
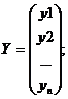

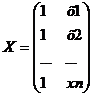 ;
; 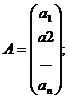
Параметры модели находятся с использованием МНК. Подсчитывается сумма квадратов ошибок наблюдений.
Метод наименьших квадратов.
Классический подход к оцениванию параметров линейной регрессии основан на метода наименьших квадратов. МНК позволяет получить такие оценки параметров а и Ь, при которых сумма квадратов отклонений фактических значений результативного признака (у) от расчетных (теоретических) ух минимальна:
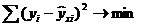
Иными словами, из свего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной: 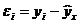 , следовательно,
, следовательно, 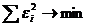
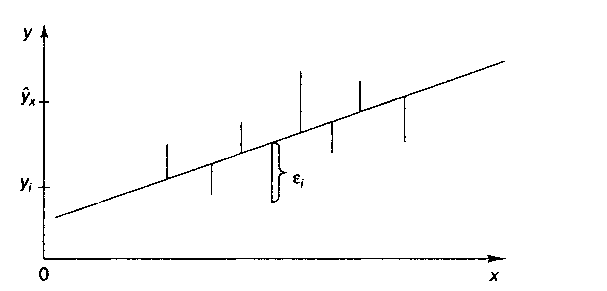
Чтобы найти минимум ф-ции 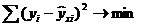 , надо вычислить частные производные по кажд. из параметров а и b и приравнять их к нулю. Обозначим
, надо вычислить частные производные по кажд. из параметров а и b и приравнять их к нулю. Обозначим 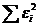 через S, тогда:
через S, тогда: 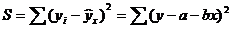 ;
;
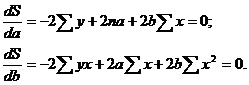
Преобразуя эту формулу, получим следующую систему нормальных уравнений для оценки параметров а и b:
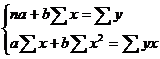
Решая эту систему нормальных уравнений либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров а и b. 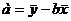 .
. 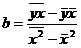
 2018-02-14
2018-02-14 384
384








